
QCL provides 4 kinds of subroutines: classical functions, pseudo-classical operators (qufunct), general unitary operators (operator) and procedures (procedure). The basic syntax for all subroutine declarations is

Since QCL allows for the inverse call of operators and can perform scratch-space management for quantum functions, the allowed side effects on the classical program state as well as on the quantum machine state have to be strictly specified.
The 4 QCL routine types form a call hierarchy, which means that a routine may invoke only subroutines of the same or a lower level (see table 2.11).
The mathematical semantic of QCL operators and functions requires that every call is reproducable. This means, that not only the program state must not be changed by these routines, but also that their execution may in no way depend on the global program state which includes global variables, options and the state of the internal random nuber generator.2.6
While QCL incorporates a classical programming language, to provides all the necessary means to change the program state, there is no hardwired set of elementary operators to manipulate the quantum machine state, since this would require assumptions about the architecture of the simulated quantum computer.
An elementary operator or qufunct can be incorporated by declaring it as extern.

The interpreter qcl includes binary versions of several common operators, including an implementation of the Fanout operator (see section 2.5.6.2) which is used by QCL scratch space management, and patterns of general unitary matrices to allow the implementation of new elementary operators.
To conveniently define a custom set of elementary operators, the external declarations can be included into the default include file default.qcl. Note that a definition of a Fanout has to be provided if local scratch variables are to be used.
For a complete list of available external operators, please refer to section 3.1.
Functions are the most restrictive routine type and don't allow any interactions with the global state.
User defined functions may be of any classic type, namely int, real, complex or string, and may take an arbitrary number of classical parameters. The value of the function is passed to the invoking routine by the return statement.
int digits(int n) { // calculate the number of
return 1+floor(log(n,2)); // binary digits of n
}
|
int fibonachi(int n) { // calculate the n-th
int a=0; // fibonachi number
int b=1; // by iteration
int i;
for i = 1 to n {
b = a+b;
a = b-a;
}
return a;
}
|
int fac(int n) { // calculate n!
if n<2 { // by recursion
return 1;
} else {
return n*fac(n-1);
}
}
|
Procedures are the most general routine type and used to implement the classical control structures of quantum algorithms which generally involve evaluation loops, the choise of applied operators, the interpretation of measurements and classical probabilistic elements.
With the exception of routine declarations, procedures allow the same operations as are available in global scope (e.g. at the shell prompt) allowing arbitrary changes to both the program and the machine state. Operations exclusive to procedures are
Procedures can take any number of classical or quantum arguments and may call all types of subroutines.
procedure prepare(qureg q) {
const l = #q/2; // use one half of the register
int i; // for the offset
reset; // initialize machine state
Mix(q[l:#q-1]); // generate periodic distribution
for i = 0 to l-1 { // randomize the offset
if 0.5<random() {
Not(q[i]);
}
}
}
|
qcl> qureg q[4]; qcl> prepare(q); [4/4] 0.5 |0010> + 0.5 |1010> + 0.5 |0110> + 0.5 |1110> qcl> prepare(q); [4/4] 0.5 |0000> + 0.5 |1000> + 0.5 |0100> + 0.5 |1100> qcl> prepare(q); [4/4] 0.5 |0011> + 0.5 |1011> + 0.5 |0111> + 0.5 |1111> |
The routine type operator is used for general unitary operators. Conforming to the mathematical notion of an operator, a call with the same parameters has to result in exactly the same transformation, so no global variable references, random elements or dependencies on input are allowed.
Since the type operator is restricted to reversible transformations of the machine state, reset and measure commands are also forbidden.
Operators work on one or more quantum registers
(register operator, see section 1.3.2.2), so
depending on the mapping of the registers, a
call of an ![]() qubit operator with a total quantum
heap of
qubit operator with a total quantum
heap of ![]() qubits can result in
qubits can result in
![]() different unitary transformations.
different unitary transformations.
In QCL, this polymorphism is even further extended by
the fact, that quantum registers can be of different
sizes, so for every quantum parameter ![]() , the
register size
, the
register size
![]() is an
implicit extra parameter of type int.
An addition to that, operators can take an arbitrary number
of explicit classical arguments.
is an
implicit extra parameter of type int.
An addition to that, operators can take an arbitrary number
of explicit classical arguments.
If more than one argument register is given, their qubits may not overlap.
qcl> qureg q[4]; qcl> qureg p=q[2:3]; qcl> CNot(q[1\2],p); ! runtime error: quantum arguments overlapping |
As allready mentioned in section 2.4.1.2, operator calls
can be inverted by the adjungation prefix `!'.
The adjoint operator to a composition of unitary operators
is2.7
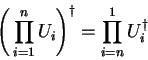 |
(2.10) |
When the adjungation flag is set, the operator body is executed and all calls of suboperators are pushed on a stack which is then processed in reverse order with inverted adjungation flags.
As opposed to pseudo-classic operators, it is in general
impossible to uncompute an unitary operator in order
to free a local register again without also destroying
the intended result of the computation.
This is a fundamental limitation of QC known as the non
cloning theorem which results from the fact that a
cloning operation i.e. a transformation with meets the condition
| (2.11) |
| (2.12) | |||
| (2.13) |
Due to the lack of a unitary copy operation for quantum states, Bennet-style scratch space management is impossible for general operators since it is based on cloning the result register.
Despite this limitation, it is possible in QCL to allocate temporary quantum registers but it is up to the programmer to properly uncompute them again. If the option -check is set, proper cleanup is verified by the simulator.
qcl> set check 1
qcl> operator foo(qureg q) { qureg p[1]; CNot(p,q); }
qcl> qureg q[1];
qcl> Mix(q);
[1/4] 0.707107 |0000> + 0.707107 |0001>
qcl> foo(q);
! in operator foo: memory error: quantum heap is corrupted
[1/4] 0.707107 |0000> + 0.707107 |0011>
|
![[*]](crossref.png) ) for an example.
) for an example.
The routine type qufunct is used for pseudo-classic
operators and quantum functions, so all transformations
have to be of the form
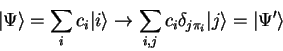 |
(2.14) |
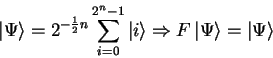 |
(2.15) |
The most straightforward application for pseudo-classic operators is the direct implementation of bijective functions (see section 1.3.3.1)
qufunct inc(qureg x) {
int i;
for i = #x-1 to 1 {
CNot(x[i],x[0:i-1]);
}
Not(x[0]);
}
|
qcl> qureg q[4]; qcl> inc(q); [4/4] 1 |0001> qcl> inc(q); [4/4] 1 |0010> qcl> inc(q); [4/4] 1 |0011> qcl> inc(q); [4/4] 1 |0100> |
When it comes to more complicated arithmetic operations,
it is often required to apply a transformation to a
register ![]() in dependence on the content of
another register
in dependence on the content of
another register ![]() .
.
If all qubits of ![]() are required to be set,
for the transformation to take place, the operator
is a conditional operator with the invariant (quconst)
enable register
are required to be set,
for the transformation to take place, the operator
is a conditional operator with the invariant (quconst)
enable register ![]() (see section 1.3.5).
(see section 1.3.5).
A simple example for a conditional operator is the
Toffoli gate
![]() or it's generalisation, the controlled not gate.
A conditional version of the above increment operator is
also easy to implement:
or it's generalisation, the controlled not gate.
A conditional version of the above increment operator is
also easy to implement:
qufunct cinc(qureg x,quconst e) {
int i;
for i = #x-1 to 1 step -1 {
CNot(x[i],x[0:i-1] & e);
}
CNot(x[0],e);
}
|
qcl> qureg q[4]; qureg e[2]; Mix(e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110000> qcl> cinc(q,e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110001> qcl> cinc(q,e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110010> qcl> cinc(q,e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110011> |
As defined in section 1.3.3.2, a quantum function ![]() is a
pseudo-classic operator with the characteristic
is a
pseudo-classic operator with the characteristic
| (2.16) |
Since, according to the above definition, quantum functions are merely ordinary pseudo-classic operators, whose specification is restricted to certain types of input states, they also use the same QCL routine type qufunct.
The following example calculates the parity of ![]() and stores it to
and stores it to ![]() :
:
qufunct parity(quconst x,quvoid y) {
int i;
for i = 0 to #x-1 {
CNot(y,x[i]);
}
}
qcl> qureg x[2]; qureg y[1]; Mix(x);
[3/3] 0.5 |000> + 0.5 |010> + 0.5 |001> + 0.5 |011>
qcl> parity(x,y);
[3/3] 0.5 |000> + 0.5 |110> + 0.5 |101> + 0.5 |011>
|
We can extend the notion of quantum functions, by also
allowing an explicit scratch register ![]() (see section 2.3.2.4)
as an optional parameter to
(see section 2.3.2.4)
as an optional parameter to ![]() , so we end up with an
operator
, so we end up with an
operator
![]() with the
characteristic
with the
characteristic
| (2.17) |
qufunct addparity(quconst x,quvoid y,quscratch s) {
parity(x,s); // write parity to scratch
x -> y; // Fanout x to y
cinc(y,s); // increment y if parity is odd
parity(x,s); // clear scratch
}
qcl2> qureg x[2]; qureg y[2]; qureg s[1]; Mix(x);
[5/8] 0.5 |00000> + 0.5 |00010> + 0.5 |00001> + 0.5 |00011>
qcl2> addparity(x,y,s);
[5/8] 0.5 |00000> + 0.5 |01110> + 0.5 |01001> + 0.5 |01111>
|
qufunct addparity2(quconst x,quvoid y) {
qureg s[1];
parity(x,s);
x -> y;
cinc(y,s);
parity(x,s);
}
qcl2> qureg x[2]; qureg y[2]; Mix(x);
[4/8] 0.5 |00000> + 0.5 |00010> + 0.5 |00001> + 0.5 |00011>
qcl2> addparity2(x,y);
[4/8] 0.5 |00000> + 0.5 |01110> + 0.5 |01001> + 0.5 |01111>
|
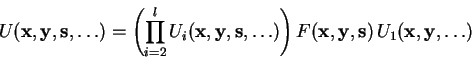 |
(2.18) |
| (2.19) |
The restriction to base-vector permutations implies that the computational path of a pure state is also a sequence of pure states, so in the case of superpositions each base-vector can be treated separately.
As shown in section 2.5.4, a arbitrary pure state
![]() can be
copied onto an empty register by a unitary
can be
copied onto an empty register by a unitary
![]() operation:
operation:
| (2.20) |
Table 2.13 shows a realisation using controlled-not gates which is mathematically equivalent to the default implementation of the external operator Fanout.
The quantum type quscratch declares a local register as managed scratch space. Managed scratch space (or junk) registers are temporary registers which are empty when allocated and automatically get uncomputed after the body of the qufunct has been applied.
So, in contrast to local qureg registers or
quscratch parameters, a local quscratch
register ![]() has not to be emptied within the
the qufunct definition but can be left dirty.
So, in order to compute some
has not to be emptied within the
the qufunct definition but can be left dirty.
So, in order to compute some ![]() , it is sufficient,
the the body of the quantum function merely implements
some operator
, it is sufficient,
the the body of the quantum function merely implements
some operator
![]() with an arbitrary junk string
with an arbitrary junk string ![]() in the scratch register.
in the scratch register.
When a quantum function with the local junk register
![]() and the body
and the body
![]() is called, an additional scratch register
is called, an additional scratch register ![]() of the same size as
of the same size as ![]() is allocated and
instead of the 3 register operator
is allocated and
instead of the 3 register operator ![]() , the 4 register
operator
, the 4 register
operator ![]() is applied, which is defined as
is applied, which is defined as
| (2.21) |
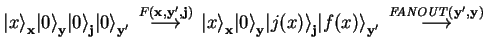 |
(2.22) | ||
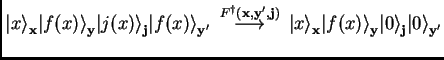 |
![[*]](crossref.png) we can construct a quantum function bitcmp which
implements a ``bit comparison'' function
we can construct a quantum function bitcmp which
implements a ``bit comparison'' function
qufunct bitcmp(quconst x1,quconst x2,quvoid y) {
const n=ceil(log(max(#x1,#x2)+1,2));
int i;
quscratch j[n]; // allocate a managed scratch register
for i=0 to #x1-1 { // j = number of bits in x1
cinc(j,x1[i]); // increment j if bit i of x1 is set
}
Not(j); // j = 2^n-j-1 = -1-j mod 2^n
for i=0 to #x2-1 { // j = j+number of bits in x2
cinc(j,x2[i]); // increment j if bit i of x1 is set
}
CNot(y,j); // set y=1 if j==2^n-1
}
qcl> qureg x1[2]; qureg x2[2]; qureg y[1];
qcl> Mix(x1[1]); Mix(x2[0]); Not(x2[1]);
[5/8] 0.5 |00001000> + 0.5 |00001100> + 0.5 |00001010> + 0.5 |00001110>
qcl> bitcmp(x1,x2,y);
[5/8] 0.5 |00001000> + 0.5 |00001100> + 0.5 |00011010> + 0.5 |00001110>
|
qcl> set log 1 qcl> bitcmp(x1,x2,y); @ CNot(qureg q=|0.......>,quconst c=|.0.....1>) @ CNot(qureg q=|.0......>,quconst c=|.......0>) @ CNot(qureg q=|0.......>,quconst c=|.0....1.>) @ CNot(qureg q=|.0......>,quconst c=|......0.>) @ Not(qureg q=|10......>) @ CNot(qureg q=|0.......>,quconst c=|.0...1..>) @ CNot(qureg q=|.0......>,quconst c=|.....0..>) @ CNot(qureg q=|0.......>,quconst c=|.0..1...>) @ CNot(qureg q=|.0......>,quconst c=|....0...>) @ CNot(qureg q=|..0.....>,quconst c=|10......>) @ Fanout(quconst a=|..0.....>,quvoid b=|...0....>) @ !CNot(qureg q=|..0.....>,quconst c=|10......>) @ !CNot(qureg q=|.0......>,quconst c=|....0...>) @ !CNot(qureg q=|0.......>,quconst c=|.0..1...>) @ !CNot(qureg q=|.0......>,quconst c=|.....0..>) @ !CNot(qureg q=|0.......>,quconst c=|.0...1..>) @ !Not(qureg q=|10......>) @ !CNot(qureg q=|.0......>,quconst c=|......0.>) @ !CNot(qureg q=|0.......>,quconst c=|.0....1.>) @ !CNot(qureg q=|.0......>,quconst c=|.......0>) @ !CNot(qureg q=|0.......>,quconst c=|.0.....1>) |
By additionally using the option -log-state, we can also trace the evolution of the machine state.
qcl> bitcmp(x1,x2,y); @ CNot(qureg q=|0.......>,quconst c=|.0.....1>) % 0.5 |00001000> + 0.5 |00001100> + 0.5 |00001010> + 0.5 |00001110> ..... % 0.5 |00001000> + 0.5 |01001100> + 0.5 |11101010> + 0.5 |00001110> @ Fanout(quconst a=|..0.....>,quvoid b=|...0....>) % 0.5 |00001000> + 0.5 |01001100> + 0.5 |11111010> + 0.5 |00001110> ..... @ !CNot(qureg q=|0.......>,quconst c=|.0.....1>) % 0.5 |00001000> + 0.5 |00001100> + 0.5 |00011010> + 0.5 |00001110> |