| (1.9) |
Since all unitary transformations are linear operators, any operation
performed on a quantum state is simultaneously applied to
all its base-vectors, thus
| (1.9) |
Since the qubits of a quantum computer constitute a possible
entangled overall state, there is - strictly speaking - no such
thing as a sub-state for particular qubits, since an ![]() qubit
state of the form
qubit
state of the form
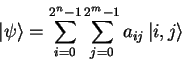 |
(1.10) |
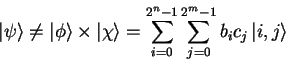 |
(1.11) |
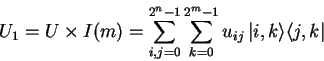 |
(1.12) |
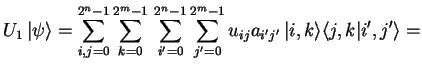 |
|||
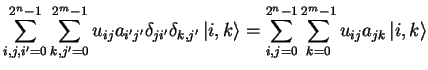 |
(1.13) |
The concept of quantum registers can be extended to arbitrary sequences of qubits.
| (1.14) |
The general form of a unitary operator ![]() over
over ![]() qubits is
qubits is
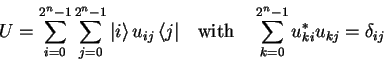 |
(1.16) |
Let
![]() be a bijective function,
then the corresponding pseudo-classic operator
be a bijective function,
then the corresponding pseudo-classic operator ![]() is given as
is given as
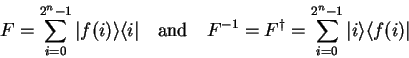 |
(1.17) |
One obvious problem of quantum computing is its restriction to
reversible computations.
Consider a simple arithmetical operation like integer division by 2
(
![]() for even
for even ![]() and
and
![]() for
odd
for
odd ![]() ).
Clearly, this operation is non-reversible since
).
Clearly, this operation is non-reversible since
![]() , so no corresponding pseudo-classic operator exists.
, so no corresponding pseudo-classic operator exists.
However, if we use a second register with the initial value ![]() ,
then we can define an operator
,
then we can define an operator ![]() witch matches the condition
witch matches the condition
![]() or
or
![]() respectively.
The behaviour of
respectively.
The behaviour of
![]() is undefined and can be set
arbitrarily under the condition that
is undefined and can be set
arbitrarily under the condition that ![]() is unitary1.6.
is unitary1.6.
While keeping a copy of the argument will allow us to compute non reversible functions, this also forces us to provide extra storage for intermediate results. In longer calculations this would leave us with a steadily increasing amount of ``junk'' bits which are of no concern for the final result.
A simple and elegant solution of this problem was proposed by Bennet
[8,9]:
If a composition of two non-reversible functions ![]() is
to be computed, the scratch space for the intermediate result
can be ``recycled'' using the following procedure (
is
to be computed, the scratch space for the intermediate result
can be ``recycled'' using the following procedure (![]() and
and ![]() are the quantum functions for
are the quantum functions for ![]() and
and ![]() , the indices indicate
the registers operated on):
, the indices indicate
the registers operated on):
| (1.18) |
Without scratch-management, the evaluation of a composition of depth
![]() needs
needs ![]() operations and consumes
operations and consumes ![]() junk registers.
Bennet's method of uncomputing can then be used to trade space
against time: Totally uncomputing of all intermediate results
needs
junk registers.
Bennet's method of uncomputing can then be used to trade space
against time: Totally uncomputing of all intermediate results
needs ![]() operations and
operations and ![]() scratch registers, which is useful,
if the scratch can be reused in the further computation.
scratch registers, which is useful,
if the scratch can be reused in the further computation.
By a combined use of ![]() registers as scratch and junk space,
a composition of depth
registers as scratch and junk space,
a composition of depth
![]() can be evaluated with
can be evaluated with
![]() operations.
An calculation of
operations.
An calculation of
![]() on a 4-register machine
(1 input, 1 output and 2 scratch/junk registers) would run as
follows (function values are in prefix notation):
on a 4-register machine
(1 input, 1 output and 2 scratch/junk registers) would run as
follows (function values are in prefix notation):
| (1.19) |
If the computation of a function ![]() fills a scratch register with the
junk bits
fills a scratch register with the
junk bits ![]() (i.e.
(i.e.
![]() ), a
similar procedure can free the register again:
), a
similar procedure can free the register again:
| (1.20) |
| (1.21) |
As pointed out in section 1.3.3.1, every invertible function
![]() has a corresponding
pseudo classic operator
has a corresponding
pseudo classic operator
![]() .
While a direct implementation of
.
While a direct implementation of ![]() is possible with any
complete set of pseudo-classic operators1.7,
the implementation as a quantum function can be substantially
more efficient.
is possible with any
complete set of pseudo-classic operators1.7,
the implementation as a quantum function can be substantially
more efficient.
If we have efficient implementations of the quantum functions
![]() and
and
![]() , then an
overwriting operator
, then an
overwriting operator ![]() can be constructed by using an
can be constructed by using an
![]() qubit scratch register.
qubit scratch register.
| (1.22) |
Classical programs allow the conditional execution of code in dependence on the content of a boolean variable (conditional branching).
A unitary operator, on the other hand, is static and
has no internal flow-control.1.8
Nevertheless, we can conditionally apply an ![]() qubit operator
qubit operator
![]() to a quantum register by using an enable
qubit and define an
to a quantum register by using an enable
qubit and define an ![]() qubit operator
qubit operator ![]()
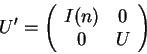 |
(1.23) |
![\begin{displaymath}
U_{[[\mathbf{e}]]}:{\vert i,\epsilon \rangle}={\vert i \ran...
...angle}_\mathbf{e} & \;\mbox{otherwise} \\
\end{array}\right.
\end{displaymath}](img152.gif) |
(1.24) |
Conditional operators a frequently used in arithmetic quantum functions and other pseudo-classic operators.
If the architecture allows the efficient implementation
of the controlled-not gate
![]() ,
then conditional pseudo-classic operators can be realised
by simply adding the enable string to the control register
of all controlled-not operations.
,
then conditional pseudo-classic operators can be realised
by simply adding the enable string to the control register
of all controlled-not operations.