To implement a computational model as a physical device, the computer must be able to adept different internal states, provide means to perform the necessary transformations on them and to extract the output information. The correlation between the physical and the logical state of the machine is arbitrary (as long it is consistent with the desired transformations) and requires interpretation.
In an ordinary RAM module, the common quantum state of thousands of
electrons is interpreted as only one bit.
The logical state is determined by the
expectation value of its register contents (e.g. tension of a
capacitor)
The interpretation as (classical) bits is performed by comparing
the measured value to a defined threshold, while the great number
of particles guarantees that the uncertainty of the measurement
is small enough (![]() ) to make errors practically impossible.
) to make errors practically impossible.
In a quantum computer, information is represented directly as the
common quantum state of many subsystems.
Each subsystem is described by a combination of two ``pure'' states
interpreted as ![]() and
and ![]() (quantum bit, qubit).
This can e.g. be realised by the spin of a particle, the
polarisation of a photon or by the ground state and an excited
state of an ion.
(quantum bit, qubit).
This can e.g. be realised by the spin of a particle, the
polarisation of a photon or by the ground state and an excited
state of an ion.
Due to the one-to-one relation between logical and physical state in a quantum computer, a quantum register containing more than one qubit can not be described by simply listing the states of each qubit. In fact, the ``state of a qubit'' becomes a meaningless term1.5
Given an isolated system of two qubits, its state can be described
by four complex amplitudes
![]() .
You can define the expectation value for the first qubit, which is
.
You can define the expectation value for the first qubit, which is
![]() but there is no isolated state for the
first qubit anymore like e.g.
but there is no isolated state for the
first qubit anymore like e.g.
![]() since
since
![]() does not implicate that
does not implicate that
![]() .
.
Therefore, manipulations on a single qubit effect the complex
amplitudes of the overall state and have a global character.
To describe the combined state
![]() of
of ![]() entangled qubits,
entangled qubits,
![]() complex numbers are necessary.
complex numbers are necessary.
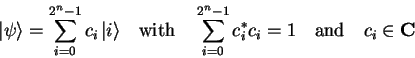 |
(1.4) |
To keep the computation coherent, quantum registers must be kept isolated, to avoid entanglement with the environment. The entropy of such a system has to remain constant since no heat dissipation is possible, therefore state changes have to be adiabatic, which requires all computations to be reversible.
Every reversible operation can be described by a unitary
operator ![]() which matches the condition
which matches the condition
![]() .
Compositions of unitary operators are also unitary since
.
Compositions of unitary operators are also unitary since
![]() .
The restriction to unitary operators can also be directly derived
for the operator of temporal propagation
.
The restriction to unitary operators can also be directly derived
for the operator of temporal propagation
![]() .
Since the Hamilton operator
.
Since the Hamilton operator ![]() is an observable it has only
real eigenvalues and
is an observable it has only
real eigenvalues and
![]() .
.
A general unitary transformation in the two dimensional Hilbert space
![]() can be defined as follows:
can be defined as follows:
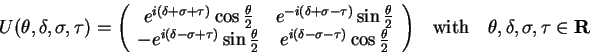 |
(1.5) |
One possibility for this operator is the 2-qubit XOR which is
defined as
![]() or in matrix
notation:
or in matrix
notation:
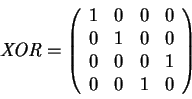 |
(1.6) |
To set a quantum computer to the desired input state
![]() ,
it suffices to provide means to initially ``cool'' all qubits to
,
it suffices to provide means to initially ``cool'' all qubits to
![]() and then apply a unitary transformation
and then apply a unitary transformation ![]() which matches
the condition
which matches
the condition
![]() .
One might think of
.
One might think of ![]() as a base transformation which trivially exists
for any desired
as a base transformation which trivially exists
for any desired
![]() .
.
Measuring ![]() qubits reduces the dimensionality of
qubits reduces the dimensionality of ![]() by a factor
of
by a factor
of ![]() .
The outcome of the measurement is biased by the probability
amplitude for a certain bit configuration.
.
The outcome of the measurement is biased by the probability
amplitude for a certain bit configuration.
Consider two quantum registers with ![]() and
and ![]() qubits in the
state
qubits in the
state
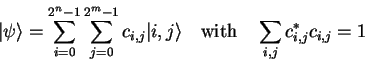 |
(1.7) |
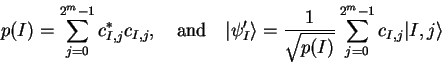 |
(1.8) |