Models of Quantum Computation

In classical information theory, the concept of the universal computer can be represented by several equivalent models, corresponding to different scientific approaches. From a mathematical point of view, a universal computer is a machine capable of calculating partial recursive functions, computer scientists often use the Turing machine as their favourite model, an electro-engineer would possibly speak of logic circuits while a programmer certainly will prefer a universal programming language.

As for quantum computation, each of these classical concepts has a quantum counterpart:

Table 1.1: classical and quantum computational models

Model	classical	quantum
Mathematical	partial recursive funct.	unitary operators
Machine	Turing Machine	QTM
Circuit	logical circuit	quantum gates
Algorithmic	univ. programming language	QCL

The Mathematical Model of QC

The moral equivalent in QC to partial recursive functions are unitary operators. As every classically computable problem can be reformulated as calculating the value of a partial recursive function, each quantum computation must have a corresponding unitary operator.

Unitary Operators

A unitary operator $U$ over the Hilbert space ${\cal H}$ is a linear operator which matches the following condition:

$$U (\alpha\,{\vert\psi \rangle}+\beta\,{\vert\phi \rangle})=\alpha\,U\,{\vert\psi \rangle}+\beta\,U\,{\vert\phi \rangle}$$

$$\quad{\rm and}\quad U^\dagger =U^{-1} \quad{\rm with}\quad {\vert\psi \rangle},\phi \in {\cal H}$$ (1.1)

While unitary operators fully describe the quantum computation itself, this would be of no use, since quantum states cannot be directly observed.

According to the Copenhagen interpretation of quantum physics, the setup and outcome of any quantum mechanical experiment must be formulated in classical terms. We thus need 2 additional Operations for setting up a defined initial state ${\vert\psi_0 \rangle}$ and for measuring the output.

Initialisation

The reset operator $\mathit{R}$ is a constant operator over ${\cal H}$ which resets a general ${\vert\psi \rangle}$ to ${\vert\psi_0 \rangle}$. Usually the base of ${\cal H}$ is chosen such that ${\vert\psi_0 \rangle}={\vert \rangle}$.

Measurement

The measurement operator $\mathit{M}(\cal{O})$ of the observable ${\cal O}=\{{\cal E}_0, {\cal E}_1, \ldots {\cal E}_k\}$, where ${\cal E}_i$ is a mutually orthogonal decomposition of ${\cal H}$, randomly applies a projection operator $P({\cal E}_m)$ to the measured state ${\vert\psi \rangle}$ biased by the probability $p_m={\langle P({\cal E}_m) \rangle}$ and renormalises the result.

The classical outcome of the measurement is $\mu(m)$ where $\mu$ is a mapping $\{0, 1, \ldots k\} \to \bf {R} \times \{ \mbox{physical unit of}\, {\cal O}\}$. ^1.1

Since the mathematical model treats unitary operators as black boxes, no complexity measure is provided.

The Machine Model of QC

In analogy to the classic Turing Machine (TM) several propositions of Quantum Turing Machines (QTM), as a model of a universal quantum computer have been made [3,1].

The complete machine-state ${\vert\Psi \rangle}$ is thereby given by a superposition of base-states ${\vert l,j,s \rangle}$, where $l$ is the inner state of the head, $j$ the head position and $s$ the binary representation of the tape-content. To keep ${\cal H}$ separable, the (infinite) bit-string $s$ has to meet the zero tail state condition i.e. only a finite number of bits with $s_m \neq 0$ are allowed.

The quantum analogon to the transition function of a classic probabilistic TM is the step operator $T$, which has to be unitary to allow for the existence of a corresponding Hamiltonian^1.2 and meet locality conditions for the effected tape-qubit, as well as for head movement.

QTMs provide a measure for execution times, but - as with the classical TM - finding an appropriate step operator can be very hard and runtime-complexity (i.e. the number of applications of $T$ in relation to the problem size) remains an issue. Outside quantum complexity theory, QTMs are of minor importance.

The Gate Model of QC

Quantum circuits are the QC equivalent to classical boolean feed-forward networks, with one major difference: since all quantum computations have to be unitary, all quantum circuits can be evaluated in both directions (as with classical reversible logic). Quantum circuits are composed of elementary gates and operate on qubits, thus $\dim({\cal H})=2^n$ where $n$ is the (fixed) number of qubits.

The actual unitary transformation performed by a $m$-qubit gate depends on the $2^m$-dimensional subspace ${\cal H}'\subseteq{\cal H}$ corresponding to the particular positions of the input qubits. Let $G$ be the 2 dimensional operator ($m=1$) of a gate operating on the $k$-th qubit of the state ${\vert\psi \rangle}\in {\cal H}= {\bf C}^{2^n}$ and $I(l)$ the $l$-qubit identity operator, then the resulting operator $G_k(n)$ is

$$G_k(n)=I(k-1) \times G \times I(n-k-1) \quad{\rm with}\quad... ... {\vert\psi \rangle},\, {\vert\psi \rangle}\in {\bf C}^{2^l}.$$ (1.2)

A quantum $m$-qubit gate in an $n$-qubit Hilbert space therefore represents a class of $\frac{n!}{(n-m)!}$ unitary operators.

To allow for implementation of all possible unitary transformations, a universal set of elementary gates must be available, out of which composed gates can be constructed. One possible set (as proposed by Deutsch) [4] is e.g. $\left\{\theta \in [0,2\pi) \left\vert D(\theta)\right.\right\}$ with

$$D(\theta):{\vert i,j,k \rangle} \to \left\{ \begin{array}{c... ...rt i,j,k \rangle} & \;\mbox{otherwise} \\ \end{array}\right.$$ (1.3)

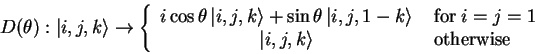However, even one $D(\theta)$ with irrational $\theta/\pi$ is sufficient, to approximate any unitary operator to arbitrary precision.^1.3

As opposed to the operator formalism, the gate-notation is an inherently constructive method and - other than QTMs - the complexity of the problem is directly reflected in the number of gates necessary to implement it.

Programming Languages

When it comes to programming and the design of non-classic algorithms, we can look at operator-algebra as the specification and quantum gates as the assembly language of QC.

The lack of typical programming techniques as local quantum variables, scratch space management and dynamic register lengths as generic features in either formalism makes the the actual implementation^1.4 of non-trivial quantum algorithms very complex and difficult (see [13] for an example) since the classical ``divide and conquer'' approach is only of limited use.

Another problem is the classical control structure: Due to their probabilistic nature, evaluation of measurements and conditional retries are part of almost any quantum algorithm, however they cannot be described within the traditional formalism.

The purpose of QCL is, to fill this gap and serve as a high-level programming language for quantum computing.

Footnotes

.... ^1.1

Since we are not interested in physical values, and ${\cal O}$ normally corresponds to a register of qubits, we can use the standard observable, so $\mu(i)=i$.

... Hamiltonian^1.2

In continuous-time quantum mechanics, the operator $U$ of temporal propagation is given by $U(t)=e^{-iH(t-t_0)/\hbar}$. Since $H$ has only real eigenvalues, $U$ must be unitary.

... precision.^1.3

Note that $D(\pi/2)$ defines the Toffoli gate, which is universal for classical reversible logic.

... implementation^1.4

This means the constructive specification of the elementary gate sequence, not its experimental realisation.