| (3.12) |
This section introduces the unitary operators needed by the Shor algorithm presented in section 3.3.
| (3.12) |
qufunct flip(qureg q) { // pseudo classic op to swap bit order
int i; // declare loop counter
for i=0 to #q/2-1 { // swap 2 symmetric bits
Swap(q[i],q[#q-i-1]);
}
}
|
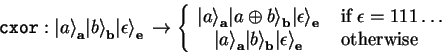 |
(3.13) |
qufunct cxor(quconst a,qureg b,quconst enable) {
int i;
for i=0 to #a-1 {
CNot(b[i],a[i] & enable);
}
}
|
Comparing two classical binary numbers ![]() and
and
![]() can be simply achieved by comparing form the
highest to the lowest bits and returning at
the first mismatch.
can be simply achieved by comparing form the
highest to the lowest bits and returning at
the first mismatch.
for i=n-1 to 0 { // check whether b<a
if bit(b,i)<bit(a,i) { return true; }
}
return false;
|
One possibility is to emulate an early return from the loop by using conditional operators (see section 1.3.5): For each bit comparison, we use an enable bit which is set to 1 if the bits are equal (and the loop has to continue) or to 0 if the result is decided and further comparisons should be disabled.
To compare an ![]() qubit register
qubit register ![]() to a classical
integer
to a classical
integer ![]() , we have to use an
, we have to use an ![]() junk register
junk register ![]() to store the enable bits.
The main loop of the quantum comparison
to store the enable bits.
The main loop of the quantum comparison ![]() then
runs a follows.
then
runs a follows.
for i=#b-2 to 1 step -1 { // continue for lower bits
if bit(a,i) { // set new junk bit if undecided
CNot(j[i-1],j[i] & b[i]);
Not(b[i]); // honour last junk bit and
CNot(flag,j[i] & b[i]); // set result flag if a[i]>b[i]
} else {
Not(b[i]);
CNot(j[i-1],j[i] & b[i]);
}
Not(b[i]); // restore b[i] again
}
|
A multiplexed adder adds one of two classical bits ![]() and
and ![]() to a qubit
to a qubit ![]() , depending on the content of a selection
qubit
, depending on the content of a selection
qubit ![]() .
The target register
.
The target register
![]() consists of a carry-in and a carry-out qubit, to allow
cascading.
The truth table for the operation is:
consists of a carry-in and a carry-out qubit, to allow
cascading.
The truth table for the operation is:
|
|
qufunct muxadd(int a0,int a1,qureg sel,quconst b,quvoid sum,quconst e) {
int i;
for i=0 to #b-2 { // fulladd first #b-1 bits
muxaddbit(bit(a0,i),bit(a1,i),sel,b[i],sum[i:i+1],e);
} // half add last bit
muxaddbit(bit(a0,#b-1),bit(a1,#b-1),sel,b[#b-1],sum[#b-1],e);
}
|
Many number theoretic algorithms describe calculations
in the remainder class ![]() .
On example for a quantum algorithm using modular arithmetic,
is Shor's method of polynomial time quantum factoring
(see section 3.3).[11].
.
On example for a quantum algorithm using modular arithmetic,
is Shor's method of polynomial time quantum factoring
(see section 3.3).[11].
For a more detailed discussion of unitary operators for modular arithmetic, please refer to [13].
The addition modulo ![]() of a classic integer
of a classic integer ![]() and
a quantum register
and
a quantum register ![]() can result in either
can result in either
![]() or
or ![]() , depending on the particular
base-vector
, depending on the particular
base-vector ![]() .
.
While for ![]() the operation is revertible, this is not
the case for
the operation is revertible, this is not
the case for ![]() , so, if
, so, if ![]() doesn't happen
to be a power of
doesn't happen
to be a power of ![]() , besides the target resister
, besides the target resister
![]() for the sum, we need an additional flag-qubit
for the sum, we need an additional flag-qubit
![]() to allow for a quantum function addn
which is both, unitary and invariant to
to allow for a quantum function addn
which is both, unitary and invariant to ![]() :
:
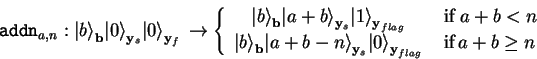 |
(3.14) |
qufunct addn(int a,int n,quconst b,quvoid flag,quvoid sum,quconst e) {
qureg s=sum[0\#b-1];
qureg f=sum[#b-1];
qureg bb=b; // "abuse" sum and b as scratch
lt(n-a,bb,f,s); // for the less-than operator
CNot(flag,f & e); // save result of comparison
!lt(n-a,bb,f,s); // restore sum and b
muxadd(2^#b+a-n,a,flag,b,sum,e); // add either a or a-n
}
|
Since
![]() is a quantum function for
modular subtraction and thus implements the inverse function
is a quantum function for
modular subtraction and thus implements the inverse function
![]() to
to
![]() ,
we can construct an overwriting version oaddn
of modular addition, by using the method introduced
in section 1.3.4.3:
,
we can construct an overwriting version oaddn
of modular addition, by using the method introduced
in section 1.3.4.3:
| (3.15) |
| (3.16) |
qufunct oaddn(int a,int n,qureg sum,quconst e) {
qureg j[#sum];
qureg f[1];
addn(a,n,sum,f,j,e); // junk -> a+b mod n
Swap(sum,j); // swap junk and sum
CNot(f,e); // toggle flag
!addn(n-a,n,sum,f,j,e); // uncompute b to zero
}
|
Modular multiplication is merely a composition of conditional
additions for each qubit of ![]() since
since
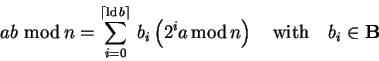 |
(3.17) |
qufunct muln(int a,int n,quconst b,qureg prod,quconst e) {
int i;
for i=0 to #prod-1 {
if bit(a,i) { CNot(prod[i],b[0] & e); }
}
for i=1 to #b-1 {
oaddn(2^i*a mod n,n,prod,b[i] & e);
}
}
|
By using two conditional XOR gates (see section 3.2.1.1)
for swapping the registers3.2we can implement a conditional
![]()
qufunct omuln(int a,int n,qureg b,quconst e) {
qureg j[#b];
muln(a,n,b,j,e);
!muln(invmod(a,n),n,j,b,e);
cxor(j,b,e);
cxor(b,j,e);
}
|
As with muln, we can construct modular exponentiation
by conditionally applying omuln with the qubits
of the exponents as enable string, according to
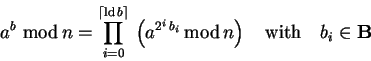 |
(3.18) |
qufunct expn(int a,int n,quconst b,quvoid ex) {
int i;
Not(ex[0]); // start with 1
for i=0 to #b-1 {
omuln(powmod(a,2^i,n),n,ex,b[i]); // ex -> ex*a^2^i mod n
}
}
|
For a ![]() dimensional vector
dimensional vector
![]() , the discrete
Fourier transform is defined as
, the discrete
Fourier transform is defined as
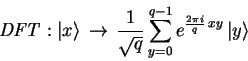 |
(3.19) |
As suggested by Coppersmith [7],
the same principle could adapted be to quantum computers
by using a combination of Hadamard transformations ![]() and
conditional phase gates
and
conditional phase gates ![]() (indices indicate the
qubits operated on):
(indices indicate the
qubits operated on):
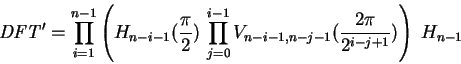 |
(3.20) |
The base-vectors of the transformed state
![]() are given in reverse
bit order, so the get the actual
are given in reverse
bit order, so the get the actual ![]() , the bits
have to be flipped.
, the bits
have to be flipped.
operator dft(qureg q) { // main operator
const n=#q; // set n to length of input
int i; int j; // declare loop counters
for i=0 to n-1 {
for j=0 to i-1 { // apply conditional phase gates
CPhase(2*pi/2^(i-j+1),q[n-i-1] & q[n-j-1]);
}
Mix(q[n-i-1]); // qubit rotation
}
flip(q); // swap bit order of the output
}
|