This section introduces the possible elementary operators, that can be used with the current implementation of QCL. Since QCL as a language doesn't enforce a specific set of elementary operators, they have to be declared as external (see section 2.5.1.3), to make them available to programs.
This is usually done within the default include file default.qcl (see appendix A.1), which is loaded at startup.
The most general form for specifying a unitary operator
(or any other linear transformation) is by defining it's
matrix elements:
An ![]() qubit unitary operator
qubit unitary operator ![]() describes a transformation
describes a transformation
![]() and therefore corresponds to
a
and therefore corresponds to
a
![]() matrix in
matrix in ![]()
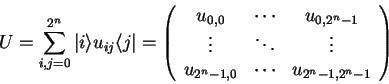 |
(3.1) |
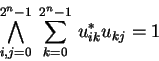 |
(3.2) |
extern operator Matrix2x2( complex u00,complex u01, complex u10,complex u11, qureg q); extern operator Matrix4x4(...,qureg q); extern operator Matrix8x8(...,qureg q); |
qcl> const i=(0,1); qcl> qureg q[1]; qcl> Matrix2x2(i*cos(pi/6),i*sin(pi/6),(0,0),(1,0),q); ! external error: matrix operator is not unitary |
The rotation of a single qubit is defined by the
transformation matrix ![]()
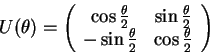 |
(3.3) |
extern operator Rot(real theta,qureg q); |
qcl> Rot(pi/2,q); ! external error: Only single qubits can be rotated |
The Hadamard Gate is a special case of a generalised
qubit Rotation and defined by the transformation matrix ![]()
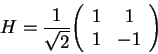 |
(3.4) |
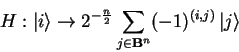 |
(3.5) |
The Hadamard Transformation is self adjoint (i.e. ![]() ),
which, for unitary operators, implies that
),
which, for unitary operators, implies that ![]() .
.
Since ![]() only contains uniform superpositions
that just differ by the signs of the base-vectors,
the external implementation of
only contains uniform superpositions
that just differ by the signs of the base-vectors,
the external implementation of ![]() id called
id called ![]() .
.
extern operator Mix(qureg q); |
The conditional phase gate is a pathological case
of a conditional operator (see section 1.3.5), for
the zero-qubit phase operator ![]() .
.
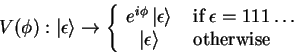 |
(3.6) |
extern operator CPhase(real phi,qureg q); |
The most general form for specifying an ![]() qubit pseudo-classic
operator
qubit pseudo-classic
operator ![]() , is by explicitly defining the underlying
permutation
, is by explicitly defining the underlying
permutation ![]() of base-vectors:
of base-vectors:
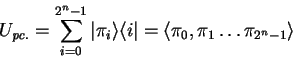 |
(3.7) |
QCL provides external operators for vector permutations
for
![]() and
and ![]() which the programmer
can use to directly implement a custom set of
which the programmer
can use to directly implement a custom set of ![]() to
to
![]() qubit pseudo-classical operators:
qubit pseudo-classical operators:
extern qufunct Perm2(int p0 ,int p1 ,qureg q); extern qufunct Perm4(int p0 ,int p1 ,int p2 ,int p3 ,qureg q); extern qufunct Perm8(...,qureg q); extern qufunct Perm16(...,qureg q); extern qufunct Perm32(...,qureg q); extern qufunct Perm64(...,qureg q); |
qcl> qureg q[3]; qcl> Perm8(0,0,1,2,3,4,5,6,q); ! external error: no permutation |
The
![]() operation is a quantum function
(see section 1.3.3.2)
and stands for a class of transformations with the
characteristic
operation is a quantum function
(see section 1.3.3.2)
and stands for a class of transformations with the
characteristic
![]() (see section 2.5.6.2 for details).
(see section 2.5.6.2 for details).
The external fanout operator of QCL is defined as
| (3.8) |
extern qufunct Fanout(quconst a,quvoid b); |
The ![]() operator exchanges the qubits of two equal
sized registers (
operator exchanges the qubits of two equal
sized registers (
![]() ).
A one to one qubit
).
A one to one qubit ![]() operator has the transformation
matrix
operator has the transformation
matrix
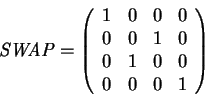 |
(3.9) |
extern qufunct Swap(qureg a,qureg b); |
The not operator ![]() inverts a qubit. Its transformation
matrix is
inverts a qubit. Its transformation
matrix is
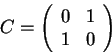 |
(3.10) |
![\begin{displaymath}
C_{[[\mathbf{e}]]}:{\vert b \rangle}{\vert\epsilon \rangle}...
...angle}_\mathbf{e} & \;\mbox{otherwise} \\
\end{array}\right.
\end{displaymath}](img333.gif) |
(3.11) |
extern qufunct Not(qureg q); extern qufunct CNot(qureg q,quconst c); |
qcl> qureg q[4]; qureg p[4]; qcl> Not(q); [8/8] 1 |00001111> qcl> CNot(p,q); [8/8] 1 |11111111> |