The memory of a quantum computer is usually a combination of 2-state subsystems, referred to as quantum bits (qubits). As pointed out in section 1.2.2 the ``memory content'' is the combined state of all qubits. This state is referred to as the (quantum) machine state as opposed to the program state which is the current state of the controlling (classic) algorithm (e.g. contents of variable, execution stack, etc.) 2.3
The machine state
![]() of an
of an ![]() qubit quantum computer is
a vector in the Hilbert space
qubit quantum computer is
a vector in the Hilbert space
![]() ,
however - due to the destructive nature of measurement
(see section 1.2.5) -
,
however - due to the destructive nature of measurement
(see section 1.2.5) -
![]() cannot be directly
observed.
cannot be directly
observed.
QCL uses the concept of quantum registers (see section 1.3.2) as an interface between the machine state and the controlling algorithm. A quantum register is a pointer to a sequence of (mutually different) qubits and all operations on the machine state (except for the reset command, see section 2.4.2.2) take quantum registers as arguments.
Since an ![]() qubit quantum computer allows for
qubit quantum computer allows for
![]() different
different ![]() qubit registers, any unitary or
measurement operation on a
qubit registers, any unitary or
measurement operation on a ![]() qubit register, can result
in
qubit register, can result
in
![]() different operations on the machine state:
different operations on the machine state:
Let ![]() be an
be an ![]() qubit register covering the qubits at
the zero-based positions
qubit register covering the qubits at
the zero-based positions
![]() (with
(with ![]() for all
for all ![]() )
of the
)
of the ![]() qubit machine state
qubit machine state
![]() and
and ![]() be a
be a
![]() qubit unitary or measurement operator, then the
register operation
qubit unitary or measurement operator, then the
register operation
![]() corresponds to
the following machine state operation (see section 1.3.2.2):
corresponds to
the following machine state operation (see section 1.3.2.2):
| (2.1) |
In QCL, the relation between registers and qubits is handled transparently by allocation and deallocation from qubits of the quantum heap, which allows the use of local quantum variables. All free (i.e. unallocated) quantum memory has to be empty.
| (2.2) |
At startup or after the reset command, the whole
machine state is empty, thus
![]() .
.
Pseudo-classic operators (qufunct) allow the use
of local quantum variables as scratch space
(see section 1.3.4).
When temporary scratch registers
(quscratch) are allocated, memory management
has to keep track of all applied operators until the
local register is deallocated again.
Then the result registers are saved using
![]() and the
computation is run in reverse.
and the
computation is run in reverse.
The user can override default memory management by explicitly exclude local variables form uncomputing by declaring them as general registers qureg (see section 2.3.2.1). In this case, proper cleanup is in the responsibility of the programmer.
While QCL - as a programming language - is designed to work with any qubit-based quantum computer architecture, the development of the necessary hardware will most probably take a few more decades. This is why QCL also supports the simulation of quantum computers and provides special commands for accessing the (simulated) machine state.
The interpreter qcl can simulate quantum computers with arbitrary numbers of qubits (option -bits). Only base-vectors with a nonzero amplitude are actually stored, so the use of scratch registers doesn't require additional memory.
All numerical simulations are handled by the QC library. Please refer to [17] for a more detailed description.
Quantum registers bound to a symbolic name are referred to as quantum variables.
A general quantum Register with
![]() qubits can be declared
with
qubits can be declared
with
A declaration in global scope defines a permanent quantum register which is not to prone to scratch space management. This means that - as with classic global variables - there is no way to reclaim allocated qubits within the same shell.
If a global register is defined in a subshell (see section 2.2.4.4) and the subshell is closed, the symbol is destroyed and the allocated qubits are again marked as free. It is up to the programmer to guarantee that the deallocated qubits are in fact empty.2.4
qcl> qureg q[1]; // allocate a qubit qcl> Rot(-pi/2,q); // perform single bit rotation [1/4] 0.707107 |0000> + 0.707107 |0001> qcl> shell; // open subshell : shell escape qcl1> qureg p[1]; // allocate another qubit qcl1> Rot(-pi/2,p); // also rotate register p [2/4] 0.5 |0000> + 0.5 |0010> + 0.5 |0001> + 0.5 |0011> qcl1> exit; // leave subshell qcl> dump; // former register p is not empty : STATE: 1 / 4 qubits allocated, 3 / 4 qubits free 0.5 |0000> + 0.5 |0010> + 0.5 |0001> + 0.5 |0011> qcl> list p; // however symbol p is undefined : symbol p is undefined. |
[0/4] 1 |0000> qcl> qureg q[1]; // allocate a qubit qcl> reset; // reset: |Psi> -> |0> [1/4] 1 |0000> qcl> list q; // register q still exists : global symbol q = |...0>: qureg q[1]; |
Registers can be declared constant, by using the register type quconst. A quantum constant has to be invariant to all applied operators.
| (2.3) |
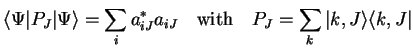 |
(2.4) | ||
| (2.5) | |||
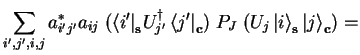 |
|||
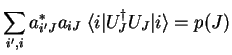 |
qcl> quconst c[1]; qcl> Mix(c); ! parameter mismatch: quconst used as non-const argument to Mix |
qcl> operator foo(quconst c) { Rot(pi,c); }
! in operator foo: parameter mismatch: quconst used as non-const
argument to Rot
|
If an argument ![]() to an operator is declared quvoid,
the quantum register is expected to be empty
when the operator is called normally (see section 2.4.1.2),
or to be uncomputed if the operator is called inverted.
So, depending on the adjungation flag of the operator,
the machine state
to an operator is declared quvoid,
the quantum register is expected to be empty
when the operator is called normally (see section 2.4.1.2),
or to be uncomputed if the operator is called inverted.
So, depending on the adjungation flag of the operator,
the machine state
![]() has to conform to either
has to conform to either
| (2.6) |
qcl> qureg q[4]; qcl> qureg p[4]; qcl> set check 1; // turn on consistency checking qcl> Rot(pi/100,p[2]); // slightly rotate one target qubit [8/8] 0.999877 |00000000> + -0.0157073 |01000000> qcl> Fanout(q,p); // p is assumed void ! in qufunct Fanout: memory error: void or scratch register not empty |
As an argument ![]() to an operator, registers of type
quscratch
are considered to be explicit scratch registers which
have to be empty when the operator is called and have
to get uncomputed before the operator terminates, so
operator and machine state have to satisfy the condition
to an operator, registers of type
quscratch
are considered to be explicit scratch registers which
have to be empty when the operator is called and have
to get uncomputed before the operator terminates, so
operator and machine state have to satisfy the condition
| (2.7) |
If a scratch register is defined within the body of a quantum function, Bennet-style uncomputing as introduced in section 1.3.4.2 is used to empty the register again (see section 2.5.5 for a detailed explanation).
Quantum functions using local scratch registers may not take general (qureg) registers as arguments.
qcl> qufunct nop(qureg q) { quscratch s[1]; }
! invalid type: local scratch registers can't be used with
qureg arguments
|
To conveniently address subregisters or combined registers (see below), quantum expressions can be named by declaring a register reference.
qcl> qureg q[8]; qcl> qureg oddbits=q[1]&q[3]&q[5]&q[7]; qcl> qureg lowbits=q[0:3]; qcl> list q,oddbits,lowbits; : global symbol q = |........76543210>: qureg q[8]; : global symbol oddbits = |........3.2.1.0.>: qureg oddbits; : global symbol lowbits = |............3210>: qureg lowbits; |
![[*]](crossref.png) )
for an example.
)
for an example.
A quantum expression is an anonymous register reference,
which can be used as an operator argument or to declare
named references (see above).
Subregisters can be addressed with the subscript operator
[![]() ].
Depending on the syntax (see table 2.9),
Single qubits are specified by their zero-based offset and
substrings are specified by the offset of the first
qubit and either the offset of the last qubit (syntax
[
].
Depending on the syntax (see table 2.9),
Single qubits are specified by their zero-based offset and
substrings are specified by the offset of the first
qubit and either the offset of the last qubit (syntax
[![]() :
:![]() ]) or the total length of the
subregister (syntax [
]) or the total length of the
subregister (syntax [![]()
\![]() ]).
]).
qcl> qureg q[8]; qcl> print q[3],q[3:4],q[3\4]; : |....0...> |...10...> |.3210...> |
qcl> int i=255; qcl> print q[floor(log(i,2))]; : |0.......> qcl> print q[floor(log(i,2))\2]; ! range error: invalid quantum subregister |
Registers can be combined with the concatenation operator
&.
If the registers overlap, an error is triggered.
qcl> print q[4:7]&q[0:3]; : |32107654> qcl> print q[2]&q[0:3]; ! range error: quantum registers overlap |