Fitness

The fitness function $f$ is used to direct the evolutionary process into a certain direction. The genetic algorithm is in fact merely a method of approximating the global maximum of $f$ in the search space of chromosome strings. The actual interpretation of this search space (the phenotypes) is packed into $f$ and doesn't concern the algorithm itself.

Linearity

As mentioned in Section 3.2.1, the optimal choice for $f$ is in a linear relation to the Hamming distance $H_{opt}$ to the optimal solution $S_{opt}$. In a more general definition of linearity, problems are also refered to as linear, when the following condition applies.

$$H(A,S_{opt})<H(B,S_{opt}) \, \Rightarrow \, f(A)>f(B), \qquad A,B \in {\bf B}^l, \quad f: {\bf B}^l \rightarrow {\bf R}$$

Nonlinearities in $f$ result in the slower convergence of the algorithm. Due to its stochastic nature, the algorithm will always eventually find a solution, but in some cases the number of necessary evaluations of $f$ can be greater than $2^l$ and the performance is worse then in a simple systematic search of ${\bf B}^l$.

Fitness and Error

In many cases, it is more natural to refer to the quality of an individual by its error instead of its fitness and use the genetic algorithm to minimises the error. As this is the case with neural networks, we will occasionally replace the fitness function $f$ by the error function $E$.

Error Function of a Neural Network

A training set ${\bf T}$ of a neural network is a set of pairs of a sample input vectors $I^{(k)}$ and its associated output vector $O^{(k)}$, which are called training patterns. If $f$ is the network function, then the error E of the network for the pattern $(I^{(k)},O^{(k)})$ is defined as

$$E_k={1\over 2} \sum_{i=1}^q (O^{(k)}_i-O_i)^2 \quad \mbox{with} \quad O=f(I^{(k)}), \quad f: {\bf S}^p \rightarrow {\bf S}^q$$

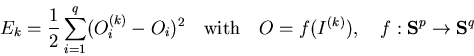
To use this definition for the genetic algorithm, the network (the phenotype) must be decoded from the chromosome string. The decoding function $d_{net}$ is inverse function of $e_{net}$ as defined in Section 2.4.4. ¹

To calculate an error for all patterns, a mean value of all $E_k$ must be calculated. If all patterns are of equal importance and a low sum of all errors is more important than a small maximum error for each pattern, then the arithmetic mean of all $E_k$ should be returned.

$$E={1\over t} \sum_{j=1}^t E_k(d_{net}(S)), \qquad t=\vert{\bf T}\vert, \quad S \in {\bf T}^l$$

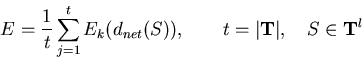
If the training set is very large and highly redundat, it is possibel to estimate the error by evaluating only a subset of ${\bf T}$ which is changed for each generation. (This can be seen as the genetic eqivalent to the backpropagation online learning described in Section 4.1.1.)

Footnotes

...neurone-types. ¹

Since $e_{net}$ maps real numbers onto strings, its inverse can in fact only return the corresponding class of networks which are mapped onto the same string, but we will gently ignore this subtlety and be content if any network of the class is returned.