The key part of the genetic algorithm if the evolutionary step of
producing a child-population ![]() out of a parent-population
out of a parent-population
![]() and thereby generating new generations of the
initial population
and thereby generating new generations of the
initial population ![]() . This process consists of two
main parts: selection and genetic transformation by
applying genetic operators to the selected individuals.
. This process consists of two
main parts: selection and genetic transformation by
applying genetic operators to the selected individuals.
The selection operator ![]() selects an individual of the given
population according to its fitness. The operator
selects an individual of the given
population according to its fitness. The operator ![]() selects a set of
selects a set of ![]() individuals and is defined as follows.
individuals and is defined as follows.
In the following examples,
![]() ,
,
![]() and the function
and the function
![]() returns a random number
of the interval
returns a random number
of the interval ![]() .
.
Since this method ignores fitness, it leads to a blind search unless used in combination with another method.
This method selects a individual
with a probability directly proportional to its fitness. The
disadvantage of this method is, that is strongly depends on the
actual definition of ![]() . A simple transformation
. A simple transformation ![]() with
a strictly monotonously increasing function
with
a strictly monotonously increasing function ![]() would result in
a different distribution.
would result in
a different distribution.
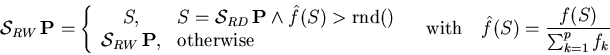
This method avoids the disadvantage of the Roulette Wheel selection
by selecting individuals according to their rank in the whole
population and thereby gaining a
fixed distribution. In the case of a linear distribution with a
uniform fraction of ![]() ,
, ![]() is defined as
is defined as
![\begin{displaymath}{\cal S}_{RS} = {\cal S}_{RW}[f'], \qquad
f'(S)={(1-u) \over...
...rt \{S' \in {\bf P} \,\vert\, f(S) \geq f(S')\} \right\vert +u \end{displaymath}](img154.gif)
This selection mechanism is used in this project, but to avoid the calculation of the ranks, the following equivalent method is used. 2
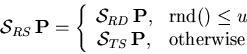
This method is often used in optimising game strategies, where two
individuals play and the winner is selected. This method can be
used even without knowing ![]() .
.
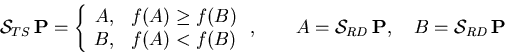
The most commonly used genetic operators are
n-point mutation (![]() ),
crossover (
),
crossover (![]() ) and
reproduction (
) and
reproduction (![]() ).
The simulation parameters
).
The simulation parameters ![]() ,
, ![]() and
and ![]() declare on how
many selected individuals of the parent generation
declare on how
many selected individuals of the parent generation ![]() each operator is applied to produce the child generation
each operator is applied to produce the child generation ![]() .
.
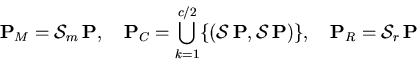
In the following definitions, the function
![]() returns a
random integer between
returns a
random integer between ![]() and
and ![]() and
and ![]() ,
, ![]() and
and ![]() are
individuals with
are
individuals with
![]() .
.
The operator ![]() inverts one bit of the individual, the
inverts one bit of the individual, the ![]() -point
mutation operator
-point
mutation operator ![]() applies
applies ![]()
![]() times. The parameter n
can be fix for the whole simulation, or be chosen randomly
each time the operator is applied.
(In this project
times. The parameter n
can be fix for the whole simulation, or be chosen randomly
each time the operator is applied.
(In this project
![]() , where
, where ![]() is a simulation parameter.)
is a simulation parameter.)
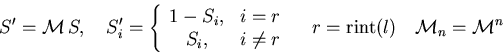
The operator ![]() exchanges the chromosome strings of two
individuals starting from a random index.
exchanges the chromosome strings of two
individuals starting from a random index.
The operator ![]() simply reproduces the individual.
simply reproduces the individual.