As in Section 3.4.3,
the error function of the training pattern
![]() is once again defined as
is once again defined as
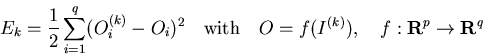
Since the network function ![]() is itself a function of the network
parameters
is itself a function of the network
parameters ![]() and
and ![]() is the set
is the set ![]() of
the weight vectors
of
the weight vectors ![]() of the
of the ![]() neurones, the error
function
neurones, the error
function ![]() is also a function of
is also a function of ![]() and a gradient can
be defined as
and a gradient can
be defined as
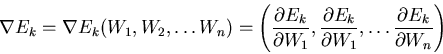
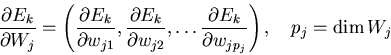
The backpropagation algorithm is a gradient descent method and thus, the weights are updated with the negative gradient of the error function.
The weights can be updated immediately after
![]() is
determined for a pattern. This is called online learning.
is
determined for a pattern. This is called online learning.
Batch Learning updates the weights with the arithmetic mean
of the corrections for all ![]() patterns. This can lead to better
results with small and very heterogeneous learn sets.
patterns. This can lead to better
results with small and very heterogeneous learn sets.
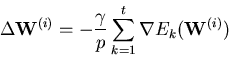
The constant ![]() is called learn rate. A high value of
is called learn rate. A high value of
![]() leads to greater learn steps at the cost of lower
accuracy.
leads to greater learn steps at the cost of lower
accuracy.
In regions where the error function is very flat, the resulting
gradient vector will be very short and lead to very small learn steps.
A solution to this problem is the introduction of an impulse
term which is added to the update
![]() and steadily
becomes greater if the direction of
and steadily
becomes greater if the direction of
![]() remains
stable.
remains
stable.
The impulse constant ![]() reflects the ``acceleration'' a point
gets on descending the error function. If we assume
reflects the ``acceleration'' a point
gets on descending the error function. If we assume ![]() as constant,
the maximum acceleration factor
as constant,
the maximum acceleration factor ![]() is given by
is given by
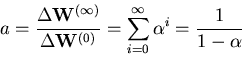
Fig. 1 shows a training process for the
XOR-problem (Section 6.2.2) with ![]() and
and
![]() .
.