Sample Problems

All sample problems deal with 2 layer networks of standard backpropagation neurones and use Boolean logic. Since the aim of this project lies mainly in quantitative comparisons, all problems are abstract, well defined and can be adapted for arbitrary problem sizes.

The variables $n$, $m$ and $o$ refer to the number of input, hidden and output nodes of an $n$-$m$-$o$-layer network. $p$ is the number of training patterns $(I^{(k)},O^{(k)})$. The problem parameters are set by upper-case command line options of the corresponding programs; if omitted, the standard values given in the right column are assumed. Only the problem specific options are given here; for general genetic, backpropagation, sequential and parallel options, please refer to the corresponding sections.

The program names of the sequential backpropagation version have the postfix - back, the sequential and parallel versions of the genetic and the combined algorithm end in - seq and - par.

N-M-N Encoder/Decoder

Source:

enc.c

problem definition

	Programs:		encseq		sequential genetic implementation
			encpar		parallel genetic implementation
			encback		sequential backpropagation implementation

	Options:		-N$n$		number of input and output nodes		$n=3$
			-M$m$		number of hidden nodes		$m=\lceil \mbox{\rm ld}n \rceil$

An $n$-$m$-$n$ encode/decoder reproduces input unit vectors at the output by finding a a compressed binary intermediate representation in the hidden layer.

$$p=n, \quad I^{(k)}_i=O^{(k)}_i=\delta_{jk}$$

The encoder/decoder problem allows big networks to be trained by a relatively small training set since the number of training patters is equal to the number of nodes.

1-Norm of a Vector

Source:

cnt.c

problem definition

	Programs:		cntseq		sequential genetic implementation
			cntpar		parallel genetic implementation
			cntback		sequential backpropagation implementation

	Options:		-N$n$		number of input nodes		$n=3$
			-M$m$		number of hidden nodes		$m=n$
			-O$o$		number of output nodes		$o=\lceil \mbox{\rm ld}n \rceil$

Counts all input nodes set to $1$ and produces the number binary encoded at the output. If the number of output nodes $o$ is set to 1, then 1 will be produced, if an odd number of inputs is set to 1, and 0 will be produced otherwise. The 1-norm can thus be seen as a generalisation of the n-parity problem. In the case of 2 input and 1 output node, this results in the 2-parity or exclusive or (XOR) problem.

$$p=2^n, \quad I^{(k)}=\mbox{\rm bin}_n k, \quad I^{(k)}=\mbox{\rm bin}_o \sum_{i=1}^n I^{(k)}_i$$

$$\mbox{with} \quad (\mbox{\rm bin}_b s)_j = \left\lfloor {s \over 2^{j-1}} \right\rfloor \bmod 1, \quad j=1, \ldots b$$

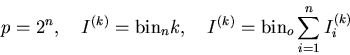
The 1-norm and the n-parity problem have both highly nonlinear error functions and are therefor a good test for the robustness of the training algorithm.

2$\times$N Comparator

Source:

cmp.c

problem definition

	Programs:		cmpseq		sequential genetic implementation
			cmppar		parallel genetic implementation
			cmpback		sequential backpropagation implementation

	Options:		-N$N$		length of one operand		$N=3$
			-M$m$		number of hidden nodes		$m=1+\left\lfloor {N \over 3} \right\rfloor$
			-Q$q$		test for $=$ if $q \neq 0$, else test for $\leq$		$q=0$

Compares the binary encoded operands $a$ and $b$ and sets the output node according to the operator determined by $q$.

$$p=2^{2N}, \quad n=2N, \quad o=1, \quad I^{(k)}=\mbox{\rm bi... ...bmod 2^N, \quad b_k=\left\lfloor {s \over 2^N} \right\rfloor$$

$$O^{(k)}_1=\left\{ \begin{array}{cl} 1, & a_k \circ_{OP} b_k... ...ray}{cl} \leq, & q=0 \\ =, & q\neq 0 \end{array} \right.$$

The 2$\times$N comparator is a relatively simple problem (at least for $q=0$) which very large ($p=2^{2N}$) and highly redundant training sets and is therefor a good test for online learning (Section 4.1.1) or error estimation (Section 3.4.3).