The main feature of backpropagation in comparison with other
gradient descent methods is, that, provided that all netto
input functions are linear, the weight update
![]() of the neurone
of the neurone ![]() can be found by using only local
information, thus information passed through the incoming and
outgoing transitions of the neurone.
This process consists of the evaluation step, where the error
is calculated and the backpropagation of the error in the
inverse direction form the output back to the input neurones.
can be found by using only local
information, thus information passed through the incoming and
outgoing transitions of the neurone.
This process consists of the evaluation step, where the error
is calculated and the backpropagation of the error in the
inverse direction form the output back to the input neurones.
Due to the linearity of the netto input function, the overall
network function ![]() consists merely of additions, scalar
multiplications and compositions of the activation functions.
The partial derivations are thus calculated as follows:
consists merely of additions, scalar
multiplications and compositions of the activation functions.
The partial derivations are thus calculated as follows:
![\begin{displaymath}{\partial{f_2\left( f_1(x) \right)}\over\partial{x}}=
{\part...
...{x}}\left[{\partial{f_2(y)}\over\partial{y}}\right]_{y=f_1(x)} \end{displaymath}](img197.gif)
During the evaluation step, not only the value of the activation function ![]() but also the value of its derivation
but also the value of its derivation ![]() is calculated for the
netto input
is calculated for the
netto input ![]() . If
. If
![]() , the derivation has a very simple form.
, the derivation has a very simple form.
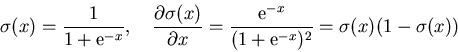
Since ![]() depends of the output vector
depends of the output vector ![]() (calculated by the network
function
(calculated by the network
function ![]() ) and only indirectly on the
weights,
) and only indirectly on the
weights, ![]() can be written as
can be written as
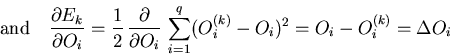
To calculate the partial derivation for each element of the weight vector
for each node, the output nodes are set to ![]() and
and
![]() is calculated by successively stepping backward in opposite direction of
the transition in
is calculated by successively stepping backward in opposite direction of
the transition in ![]() and applying the above listed derivation rules.
Composition is handled by multiplying the stored outer derivation
and applying the above listed derivation rules.
Composition is handled by multiplying the stored outer derivation ![]() onto
the sum of the inner derivations
onto
the sum of the inner derivations ![]() received via the
received via the ![]() inverted
output transitions.
inverted
output transitions.
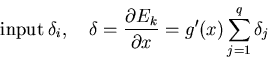
Then, ![]() is propagated to the
is propagated to the ![]() input nodes by multiplying it with
the corresponding weight
input nodes by multiplying it with
the corresponding weight ![]() . Then the weight is updated.
. Then the weight is updated.