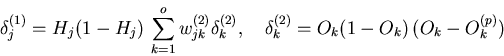As shown in Section 3.2.3, for standard backpropagation neurones
(Section 2.4.4) the parameters of a ![]() -
-![]() -
-![]() -network
can be described by two real weight matrices
-network
can be described by two real weight matrices ![]() and
and ![]() of the
dimensions
of the
dimensions
![]() and
and
![]() .
Let the vectors
.
Let the vectors ![]() ,
, ![]() and
and ![]() refer to the states of the input, hidden and
output neurones and
refer to the states of the input, hidden and
output neurones and ![]() and
and ![]() to the actual training pattern.
The weight updates
to the actual training pattern.
The weight updates
![]() and
and
![]() without impulse can
then be calculated as follows.
without impulse can
then be calculated as follows.