Since neural networks can merely be seen a function networks, neurone types
are classified by the type of their propagation function.
The propagation function ![]() of a neurone
of a neurone ![]() is normally of the form
is normally of the form
The function ![]() is called the netto input function of the neurone
is called the netto input function of the neurone ![]() , and
maps the input states onto a single real value.
The function
, and
maps the input states onto a single real value.
The function ![]() is called activation function, is usually the same for all
neurones and maps the real netto input back onto
is called activation function, is usually the same for all
neurones and maps the real netto input back onto ![]() .
.
Since most learn algorithm train the network by iteratively changing the netto input functions of the neurones, they can be written as
where ![]() is a vector of function parameters, which is to be
determined by the learn algorithm. Normally, each input node
is a vector of function parameters, which is to be
determined by the learn algorithm. Normally, each input node ![]() of the neurone
of the neurone ![]() is associated with a parameter
is associated with a parameter ![]() called its weight.
Often, there is an extra parameter, called threshold or bias.
called its weight.
Often, there is an extra parameter, called threshold or bias.
A very common definition of the netto input, is a weighted sum (a dot product) to which the bias is added.
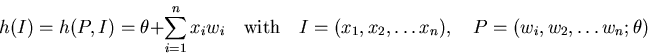
A convenient way to store the weights for ![]() -layer networks
is by replacing the adjacence matrix
-layer networks
is by replacing the adjacence matrix ![]() by the weight matrix
by the weight matrix
![]() , which contains the weights the input nodes or
, which contains the weights the input nodes or ![]() if there
is no connection.
if there
is no connection.
The activation function ![]() is normally a monotone, nonlinear function to
rescale the netto input to
is normally a monotone, nonlinear function to
rescale the netto input to ![]() , which is usually a limited interval.
If
, which is usually a limited interval.
If
![]() and
and
![]() , then
, then ![]() uses binary logic,
if
uses binary logic,
if
![]() and
and
![]() , then
, then ![]() uses bipolar logic.
uses bipolar logic.
The two most commonly used activation functions for binary logic are
the step- or ![]() -function and the sigmoide function
-function and the sigmoide function ![]() .
.
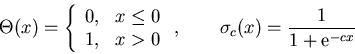
In the following examples, ![]() stands for the set
stands for the set ![]() ,
,
![]() is the set of integer numbers and
is the set of integer numbers and ![]() the set of real numbers.
All neurones are assumed to have
the set of real numbers.
All neurones are assumed to have ![]() inputs.
inputs. ![]() stands for
stands for
![]() .
.
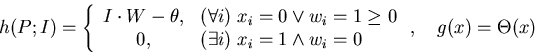
This type of neurone is very often used with the backpropagation algorithm
and also the main type for this project. No explicit ![]() is defined,
however, the effect of the bias can be achieved by simply adding an
extra neurone to each layer with a constant propagation function of
is defined,
however, the effect of the bias can be achieved by simply adding an
extra neurone to each layer with a constant propagation function of ![]() .
.