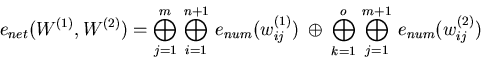The genotype ![]() of an individual
of an individual ![]() is its chromosome string, while its phenotype
is its chromosome string, while its phenotype
![]() is the representation of the problem, the user originally wants to solve.
Since the genetic algorithm operates only on the genotype, a function
must be provided to translate
is the representation of the problem, the user originally wants to solve.
Since the genetic algorithm operates only on the genotype, a function
must be provided to translate ![]() into
into ![]() .
.
How this encoding is done, depends on the type of the problem parameters ![]() and
no fixed rules can be given. A encoding is optimal if the relation between
the fitness
and
no fixed rules can be given. A encoding is optimal if the relation between
the fitness ![]() of a individual
of a individual ![]() is in a linear relation to the Hamming
distance between
is in a linear relation to the Hamming
distance between ![]() and
and ![]() , when
, when ![]() represents the genotype of
the optimal solution:
represents the genotype of
the optimal solution:
Since the ![]() in normally not known, the general strategy should be, that
similar phenotypes should also have a small Hamming distance between their
corresponding genotypes. Moreover, related groups of parameters should be
encoded in subsequent substrings of the genotype.
in normally not known, the general strategy should be, that
similar phenotypes should also have a small Hamming distance between their
corresponding genotypes. Moreover, related groups of parameters should be
encoded in subsequent substrings of the genotype.
While Boolean parameters of the phenotype ![]() can be directly encoded by mapping
them onto the chromosome string
can be directly encoded by mapping
them onto the chromosome string ![]() , the encoding of integer and real values
is not so straightforward.
, the encoding of integer and real values
is not so straightforward.
Using binary numbers for the encoding of integers of the range
![]() , leads to the problem, that the encoding of two successive
numbers
, leads to the problem, that the encoding of two successive
numbers ![]() and
and ![]() may have a Hamming distance up to
may have a Hamming distance up to ![]() .
.
The Grey code encodes the successor ![]() of an integer
of an integer ![]() by inverting
one digit of
by inverting
one digit of
![]() , and is defined by the following conditions.
, and is defined by the following conditions.
A real value ![]() can be mapped onto
can be mapped onto ![]() and
then be Grey encoded as
and
then be Grey encoded as ![]() -bit strings. The mapping function
-bit strings. The mapping function ![]() must be strictly monotonous and its return values should be
uniformly distributed. For already uniformly distributed
parameters,
must be strictly monotonous and its return values should be
uniformly distributed. For already uniformly distributed
parameters, ![]() should be defined as
should be defined as
If the genetic algorithm is to be used for the training of neural
networks, the phenotype ![]() is the set of network parameters which are
to be optimised, namely the set of the parameter vectors
is the set of network parameters which are
to be optimised, namely the set of the parameter vectors ![]() of all
neurones in
of all
neurones in ![]() .
.
The main network type used in this project is a 2-layer network which is fully interconnected except for one extra neurone in the input and the hidden (the second) layer which has no inputs and is constantly set to 1. The other neurones are either input or standard backpropagation neurones as described in Section 2.4.4.
Thus, the parameters of a ![]() -
-![]() -
-![]() -network can be described by two real
weight matrices
-network can be described by two real
weight matrices ![]() and
and ![]() of the dimensions
of the dimensions
![]() and
and
![]() . If we decide to use Grey code with a precision of
. If we decide to use Grey code with a precision of ![]() bit,
restrict the possible weight values to the interval
bit,
restrict the possible weight values to the interval ![]() and
assume them to be uniformly distributed, then
the encoding function
and
assume them to be uniformly distributed, then
the encoding function ![]() for weights can be defined as
for weights can be defined as
The encoding function ![]() for the whole network is very straightforward and
simply concatenates all parameters. The input weights of one neurone are encoded
together as one coherent substring.
for the whole network is very straightforward and
simply concatenates all parameters. The input weights of one neurone are encoded
together as one coherent substring.