Chromosome Strings

A Chromosome String is a fixed length string of a genetic alphabet ${\bf A}$.

$$S=(d_0,d_1, \ldots d_n), \qquad S \in {\bf A}^n, \qquad d_i \in {\bf A}$$

The function $\mbox{\rm len}$ returns the length of a string, the operator $\oplus$ concatenates two strings.

$$S=(d_0,d_1, \ldots d_n) \Longrightarrow \mbox{\rm len}S = n$$

$$A=(a_1,a_2, \ldots a_n), \, B=(b_1,b_2, \ldots b_m) \Longrightarrow A \oplus B = (a_1,a_2, \ldots a_n,b_1,b_2, \ldots b_m)$$

If $A=\{0,1\}$ then the Hamming distance $H$ between two string of the same length is define as

$$H(A,B) = \sum_{i=1}^n \vert A_i-B_i\vert \quad \mbox{with} \quad \mbox{\rm len}A=\mbox{\rm len}B=n$$

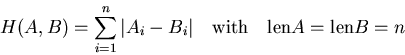
From now on, we will assume that the genetic alphabet is always $\{0,1\}$.