The memory of a quantum computer is usually a combination
of 2-state subsystems, referred to as quantum bits (qubits).
As pointed out in 2.2.1.3 the ``memory content''
is the combined state
![]() of all qubits.
This state is referred to as the (quantum) machine state
as opposed to the program state which is the
current state of the controlling (classic) algorithm
(e.g. contents of variable, execution stack, etc.)
described by the QCL program.
of all qubits.
This state is referred to as the (quantum) machine state
as opposed to the program state which is the
current state of the controlling (classic) algorithm
(e.g. contents of variable, execution stack, etc.)
described by the QCL program.
The machine state
![]() of an
of an ![]() qubit quantum computer is
a vector in the Hilbert space
qubit quantum computer is
a vector in the Hilbert space
![]() ,
however -- due to the destructive nature of measurement
(see 1.3.2.3) --
,
however -- due to the destructive nature of measurement
(see 1.3.2.3) --
![]() cannot be directly
observed and consequently isn't accessible from within
QCL.
cannot be directly
observed and consequently isn't accessible from within
QCL.
Due to the current lack of real-live quantum computers, the interpreter qcl contains the emulation library libqc which can simulate a quantum computer with an arbitrary number of qubits. It also provides an interface to access the simulated machine state via the load, save and dump commands (see 3.3.1.6). These commands, however don't interfere with the program state.
QCL uses the concept of quantum registers (see 2.2.1.5) as an interface between the machine state and the controlling classical computer. A quantum register is a pointer to a sequence of (mutually different) qubits and thus, while referring to a quantum subsystem, is still a classical variable.
All operations on the machine state (except for the reset
command, see 3.4.1) take quantum registers as
operands.
Since an ![]() qubit quantum computer allows for
qubit quantum computer allows for
![]() different
different ![]() qubit registers
qubit registers
![]() , any unitary or
measurement operation on a
, any unitary or
measurement operation on a ![]() qubit register, can result
in
qubit register, can result
in
![]() different operations on the machine state:
This requires that all elementary unitary operations of the
quantum computer to be applicable to arbitrary qubits and
requires the physical architecture to allow the measurement
of single qubits.3.2
different operations on the machine state:
This requires that all elementary unitary operations of the
quantum computer to be applicable to arbitrary qubits and
requires the physical architecture to allow the measurement
of single qubits.3.2
In QCL, the relation between registers and qubits is handled transparently by allocation and deallocation of qubits from the quantum heap, which allows the use of local quantum variables. All free (i.e. unallocated) quantum memory has to be empty.
| (3.4) |
The machine state of an ![]() -qubit quantum computer with
-qubit quantum computer with
![]() allocated qubits therefor is a product state of the
form
allocated qubits therefor is a product state of the
form
| (3.5) |
As has been pointed out in 1.3.3.2, two quantum
systems whose common wave function is a product state
are physically independent.
This esp. means that neither measurements nor unitary
transformations on the allocated bits ![]() will
affect
will
affect
![]() being in substate
being in substate ![]() .
.
The concept of the quantum heap allows two important abstractions:
Quantum registers are allocated, when a quantum variable is defined. The qubit positions for each register can be inspected using the print statement.
$ qcl -b10 # start qcl-interpreter with 10 qubits qcl> qureg a[4]; // allocate a 4-qubit register qcl> qureg b[3]; // allocate another 3-qubit register qcl> print a,b; // show actual qubit mappings : |......3210> |...210....> qcl> qureg c[5]; // try to allocate another 5 qubits ! memory error: not enough quantum memory |
qcl> qureg a[3]; // allocate 3 qubits
qcl> procedure foo() { qureg b[2]; print a,b; }
qcl> foo(); // temp. register b gets allocated
: |.......210> |.....10...>
qcl> qureg c[3]; // allocate another 3 qubits
qcl> print a,c; // qubits from b have been reclaimed
: |.......210> |....210...>
|
If temporary registers are used, then, in order to avoid the corruption of the quantum heap, it has to be assured that the register is empty befor it is deallocated. Quantum functions (see 2.2.2.5) allow the declaration of local quantum variables as scratch space (see 3.3.1.5), in which case the ``uncomputing'' of the temporary registers is transparently taken care of by using the following procedure suggested by Bennet: [8]
Let ![]() be a quantum function with the argument register
be a quantum function with the argument register ![]() (type quconst, see 3.3.2.2), the target register
(type quconst, see 3.3.2.2), the target register
![]() (type quvoid, see 3.3.2.3)
and the scratch register
(type quvoid, see 3.3.2.3)
and the scratch register ![]() (type quscratch, see
3.3.2.4)
(type quscratch, see
3.3.2.4)
| (3.6) |
| (3.7) |
| (3.8) |
| (3.9) |
The interpreter qcl can simulate quantum computers with arbitrary numbers of qubits. According to the hybrid architecture as introduced in 3.1.3, the numerical simulations are handled by a library (libqc) to separate the classical program state from the quantum machine state. QCL provides special commands for inspecting the simulated machine state.
The dump command prints the current machine state in Braket notation. When a quantum expression is given, it prints the probability spectrum instead.
qcl> qureg q[2]; qcl> Mix(q); qcl> dump; : STATE: 2 / 4 qubits allocated, 2 / 4 qubits free 0.5 |0000> + 0.5 |0010> + 0.5 |0001> + 0.5 |0011> qcl> dump q[0]; : SPECTRUM q[0]: |...0> 0.5 |0> + 0.5 |1> |
Quantum registers bound to a symbolic name are referred to as quantum variables.
A general quantum Register with
![]() qubits can be declared
with
qubits can be declared
with
A global declaration defines a permanent quantum register which is not to prone to scratch space management. This means that -- as with classic global variables -- there is no way to reclaim allocated qubits within the same scope.
The reseting of the machine state with the reset command has no effect on register bindings.
[0/4] 1 |0000> qcl> qureg q[1]; // allocate a qubit qcl> reset; // reset: |Psi> -> |0> [1/4] 1 |0000> qcl> list q; // register q still exists : global symbol q = |...0>: qureg q[1]; |
Registers can be declared constant, by using the register type quconst. A quantum constant has to be invariant to all applied operators.
| (3.10) |
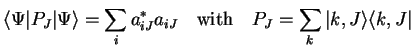 |
(3.11) | ||
| (3.12) | |||
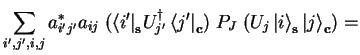 |
|||
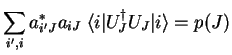 |
qcl> operator foo(quconst c) { Rot(pi,c); }
! in operator foo: parameter mismatch: quconst used as non-const
argument to Rot
|
If an argument ![]() to an operator is declared quvoid,
the quantum register is expected to be empty
when the operator is called normally,
or to be uncomputed if the operator is called inverted
(see 3.4.3.2).
So, depending on the adjungation flag of the operator,
the machine state
to an operator is declared quvoid,
the quantum register is expected to be empty
when the operator is called normally,
or to be uncomputed if the operator is called inverted
(see 3.4.3.2).
So, depending on the adjungation flag of the operator,
the machine state
![]() has to conform to either
has to conform to either
| (3.13) |
qcl> qureg q[4]; qcl> qureg p[4]; qcl> set check 1; // turn on consistency checking qcl> Rot(pi/100,p[2]); // slightly rotate one target qubit [8/8] 0.999877 |00000000> + -0.0157073 |01000000> qcl> Fanout(q,p); // p is assumed void ! in qufunct Fanout: memory error: void or scratch register not empty |
As an argument ![]() to an operator, registers of type
quscratch
are considered to be explicit scratch registers which
have to be empty when the operator is called and have
to get uncomputed before the operator terminates, so
operator and machine state have to satisfy the condition
to an operator, registers of type
quscratch
are considered to be explicit scratch registers which
have to be empty when the operator is called and have
to get uncomputed before the operator terminates, so
operator and machine state have to satisfy the condition
| (3.14) |
Quantum functions using local scratch registers may not take general (qureg) registers as arguments.
qcl> qufunct nop(qureg q) { quscratch s[1]; }
! invalid type: local scratch registers can't be used with
qureg arguments
|
To conveniently address subregisters or combined registers (see below), quantum expressions can be named by declaring a register reference.
qcl> qureg q[8]; qcl> qureg oddbits=q[1]&q[3]&q[5]&q[7]; qcl> qureg lowbits=q[0:3]; qcl> list q,oddbits,lowbits; : global symbol q = |........76543210>: qureg q[8]; : global symbol oddbits = |........3.2.1.0.>: qureg oddbits; : global symbol lowbits = |............3210>: qureg lowbits; |
A quantum expression is an anonymous register reference,
which can be used as an operator argument or to declare
named references (see above).
Subregisters can be addressed with the subscript operator
[![]() ].
Depending on the syntax (see table 3.5),
single qubits are specified by their zero-based offset and
substrings are specified by the offset of the first
qubit and either the offset of the last qubit (syntax
[
].
Depending on the syntax (see table 3.5),
single qubits are specified by their zero-based offset and
substrings are specified by the offset of the first
qubit and either the offset of the last qubit (syntax
[![]() :
:![]() ]) or the total length of the
subregister (syntax [
]) or the total length of the
subregister (syntax [![]()
\![]() ]).
]).
qcl> qureg q[8]; qcl> print q[3],q[3:4],q[3\4]; : |....0...> |...10...> |.3210...> |
qcl> int i=255; qcl> print q[floor(log(i,2))]; : |0.......> qcl> print q[floor(log(i,2))\2]; ! range error: invalid quantum subregister |
Registers can be combined with the concatenation operator
&.
If the registers overlap, an error is triggered.
qcl> print q[4:7]&q[0:3]; : |32107654> qcl> print q[2]&q[0:3]; ! range error: quantum registers overlap |