A classical, as well as a quantum computer, essentially consists of 3 parts: a memory, which holds the current machine state, a processor, which performs elementary operations on the machine state, and some sort of input/output which allows to set the initial state and extract the final state of the computation.
The quantum analogy to the classical bit is the quantum bit or qubit. Just as a classical bit is represented by a system which can adopt one of two distinct states ``0'' and ``1'' we can define a quantum bit as follows:
The general state
![]() of a qubit is given by
of a qubit is given by
| (2.2) |
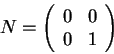 |
(2.3) |
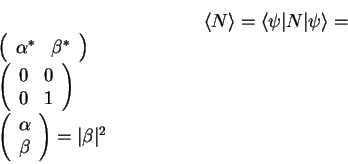 |
(2.4) |
If we combine 2 qubits, the general state of the resulting system
is
| (2.5) |
| (2.6) |
| (2.7) |
If we measure ![]() in the first qubit, the resulting
post-measurement states are
in the first qubit, the resulting
post-measurement states are
| (2.8) |
| (2.9) |
While the state of a classical computer can be given as the distinct states of all bits in memory and processor registers, the ``state of a qubit'' is a meaningless term, if the machine state is the combined state of more than one system.2.3
Generally, the machine state ![]() of an
of an ![]() -qubit quantum
computer is given by
-qubit quantum
computer is given by
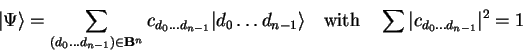 |
(2.10) |
| (2.11) |
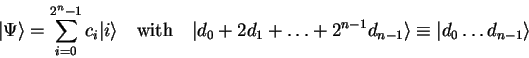 |
(2.12) |
| (2.13) |
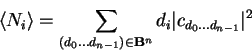 |
(2.14) |
As we have shown above, the memory of an ![]() -qubit quantum computer
is a combined system of
-qubit quantum computer
is a combined system of ![]() identical qubit-subsystems.
Since the partition into subsystems is merely methodical, we can
consider the first
identical qubit-subsystems.
Since the partition into subsystems is merely methodical, we can
consider the first ![]() qubits (
qubits (![]() ) as a single subsystem
and write
) as a single subsystem
and write ![]() as
as
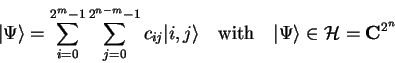 |
(2.15) |
| (2.16) |
A unitary transformation ![]() over the first
over the first ![]() qubits also
doesn't affect a measurement of the remaining qubits since
the probability
qubits also
doesn't affect a measurement of the remaining qubits since
the probability ![]() to measure
to measure ![]() in the remaining
in the remaining
![]() qubits, i.e. to get a post-measurement state of the
form
qubits, i.e. to get a post-measurement state of the
form
![]() , is invariant to
, is invariant to
![]() , as
, as
The above notion of ![]() -qubit subsystems can easily be extended
to arbitrary sequences of qubits.
-qubit subsystems can easily be extended
to arbitrary sequences of qubits.
Let ![]() be an
be an ![]() qubit register of the
qubit register of the ![]() qubit state
qubit state
![]() .
Using an arbitrary permutation
.
Using an arbitrary permutation ![]() over
over ![]() elements with
elements with
![]() for
for ![]() , we can construct a unitary
reordering operator
, we can construct a unitary
reordering operator
![]() by permutating the qubits.
by permutating the qubits.
| (2.19) |
Unitary operators correspond to base transformations (see
1.3.2.6), so we can write
![]() as
as
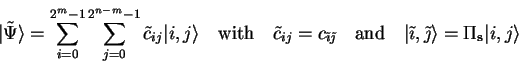 |
(2.20) |
| (2.21) |
Let ![]() be a
be a ![]() -qubit unitary operator over
-qubit unitary operator over
![]() and
and
![]() with
with ![]() being the
being the ![]() -qubit identity operator.
-qubit identity operator.
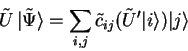 |
(2.22) |
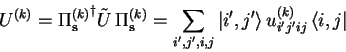 |
(2.23) |
| (2.24) |
Just as with single qubits, we can define an observable ![]() for a given
for a given ![]() -qubit register
-qubit register ![]() with the operator
with the operator
| (2.25) |
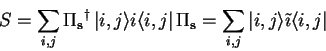 |
(2.26) |
In a classical ![]() -bit computer, every computational step can
be described by a transition function
-bit computer, every computational step can
be described by a transition function
![]() which takes the current state
which takes the current state ![]() of all bits as input and
returns the appropriate post-instruction state
of all bits as input and
returns the appropriate post-instruction state ![]() .
.
As we have shown in 1.3.2.6, the temporal evolution of a
quantum system can be described by unitary operators.
The general form of a ![]() -qubit unitary operator
-qubit unitary operator ![]() over the
Hilbert space
over the
Hilbert space
![]() is
is
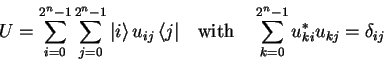 |
(2.27) |
If we compare boolean functions to unitary operators from a strictly functional point of view we can identify three major differences between classical and quantum operations:
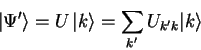 |
(2.28) |
| (2.29) |
| (2.30) |
The basic instructions of a classical computer usually operate
only on a very small number of bits and are typically independent
from the total amount of available memory.
Therefor it is more useful to describe those instructions not
as boolean functions ![]() over the whole state space
over the whole state space ![]() (in the case of an
(in the case of an ![]() bit machine), but as parameterized functions
bit machine), but as parameterized functions
![]() over
over ![]() , where the vector
, where the vector
![]() only holds the bit-positions of the relevant arguments.
Consequently we refer to the resulting instruction
only holds the bit-positions of the relevant arguments.
Consequently we refer to the resulting instruction ![]() as ``applying f
to the bits
as ``applying f
to the bits
![]() ''.
''.
While it is clear what we mean by e.g. ``swapping the bits 3 and 5'' on a classical computer, we cannot blindly adopt this concept to quantum computing, because unitary operators operate on states and a single qubit doesn't have a state.2.5
In 2.2.1.5 we have defined a quantum
register as a sequence of (mutually different) qubit-positions
![]() , which is the quantum
analogon to the above argument vector
, which is the quantum
analogon to the above argument vector ![]() , and a class
of
, and a class
of ![]() reordering operators
reordering operators
![]() which meet
the condition
which meet
the condition
| (2.31) |
| (2.32) |
So
![]() is what we actually
mean, by ``application of operator
is what we actually
mean, by ``application of operator ![]() to quantum register
to quantum register
![]() ''.
Since there are
''.
Since there are
![]() possible
possible ![]() -qubit registers
on an
-qubit registers
on an ![]() -qubit machine, a given
-qubit machine, a given ![]() -qubit operator
-qubit operator ![]() can describe
can describe
![]() different transformations
different transformations
![]() .
.
In analogy to boolean networks, unitary operators which can be applied to arbitrary sets of qubits are also referred to as quantum gates.
A well known result from classical boolean logic, is that
any possible function
![]() can be
constructed as a composition from a small universal set
of operators if we can ``wire'' the inputs and outputs to
arbitrary bits in a feed-forward network.
Examples for universal sets of logical gates are
can be
constructed as a composition from a small universal set
of operators if we can ``wire'' the inputs and outputs to
arbitrary bits in a feed-forward network.
Examples for universal sets of logical gates are
![]() ,
, ![]() or
or
![]() .
.
As mentioned in 1.3.2.6, unitary operations can
be described as abstract ``rotations'' in the Hilbert space.
A complex rotation of a single qubit has the general form
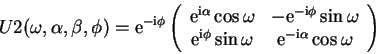 |
(2.33) |
In our definition of quantum gates, however, we are restricted
to subspaces corresponding to quantum registers (see 2.2.1.5),
so in the case of an ![]() -qubit quantum computer (
-qubit quantum computer (
![]() ),
this leaves us with merely
),
this leaves us with merely ![]() possible 1-qubit subspaces
possible 1-qubit subspaces ![]() and the corresponding sets of register operators
and the corresponding sets of register operators
![]() .
Since
.
Since
![]() , any composition
, any composition ![]() of
of ![]() gates,
would result in a transformation of the form
gates,
would result in a transformation of the form
| (2.34) |
So just as the ![]() gate itself is not universal for
boolean logic, to construct a universal set of quantum gates,
we require an additional 2-qubit operation, to
create entangled multi-qubit states.
gate itself is not universal for
boolean logic, to construct a universal set of quantum gates,
we require an additional 2-qubit operation, to
create entangled multi-qubit states.
One possibility for a nontrivial 2-qubit operator is XOR which is
defined as
![]() or in matrix
notation:
or in matrix
notation:
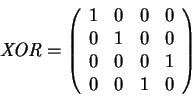 |
(2.35) |
Deutsch [6] has shown that the set
![]() is in fact
universal for unitary transformation.
Furthermore, since
is in fact
universal for unitary transformation.
Furthermore, since
![]() is dense in
is dense in
![]() for almost
any2.6set of parameters,
for almost
any2.6set of parameters,
![]() is universal for most
is universal for most ![]() in the sense
that any unitary transformation
in the sense
that any unitary transformation ![]() can be approximated to
arbitrary precision.
can be approximated to
arbitrary precision.
Deutsch also proposed a 3-qubit gate ![]() which is
universal, while only requiring one parameter:
which is
universal, while only requiring one parameter:
The general form of a unitary operator ![]() over
over ![]() qubits is
qubits is
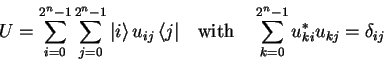 |
(2.37) |
For ![]() the universal Deutsch gate
the universal Deutsch gate ![]() (2.36) degenerates into the pseudo-classic operator
(2.36) degenerates into the pseudo-classic operator
| (2.38) |
Let
![]() be a bijective function,
then the corresponding pseudo-classic operator
be a bijective function,
then the corresponding pseudo-classic operator ![]() is given as
is given as
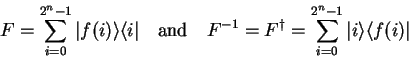 |
(2.39) |
One obvious problem of quantum computing is its restriction to
reversible computations.
Consider a simple arithmetical operation like integer division by 2
(
![]() for even
for even ![]() and
and
![]() for
odd
for
odd ![]() ).
Clearly, this operation is non-reversible since
).
Clearly, this operation is non-reversible since
![]() , so no corresponding pseudo-classic operator exists.
, so no corresponding pseudo-classic operator exists.
However, if we use a second register with the initial value ![]() ,
then we can define an operator
,
then we can define an operator ![]() which matches the condition
which matches the condition
![]() or
or
![]() respectively.
The behavior of
respectively.
The behavior of
![]() is undefined and can be set
arbitrarily as long as
is undefined and can be set
arbitrarily as long as ![]() remains pseudo-classic.2.7.
remains pseudo-classic.2.7.
For any boolean function
![]() there exist
there exist
![]() different quantum functions
different quantum functions ![]() .
.
Classical programs allow the conditional execution of code in dependence on the content of a boolean variable (conditional branching).
A unitary operator, on the other hand, is static and
has no internal flow-control.
Nevertheless, we can conditionally apply an ![]() qubit operator
qubit operator
![]() to a quantum register by using an enable
qubit and define an
to a quantum register by using an enable
qubit and define an ![]() qubit operator
qubit operator ![]()
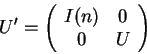 |
(2.40) |
![\begin{displaymath}
U_{[[\mathbf{e}]]}:{\vert i,\epsilon \rangle}={\vert i \ran...
...\rangle}_\mathbf{e} & \;\mbox{otherwise}
\end{array}\right.\end{displaymath}](img445.gif) |
(2.41) |
Conditional operators a frequently used in arithmetic quantum functions and other pseudo-classic operators.
If the architecture allows the efficient implementation
of the controlled-not gate
![]() ,
then conditional pseudo-classic operators can be realized
by simply adding the enable string to the control register
of all controlled-not operations.
,
then conditional pseudo-classic operators can be realized
by simply adding the enable string to the control register
of all controlled-not operations.
In 2.1.3 we have shown that the interpretation of computing as a physical process, rather than the abstract manipulation of symbols, leads to an extended notion of computability. We have also identified the the concept of unitary transformations as an adequate paradigm for ``physical computability''.
Unitary transformations describe the transition between machine states and thereby the temporal evolution of a quantum system. The very notion of a (quantum) computer as a ``computing machine'' requires, however, that the evolution of the physical system corresponds to a processing of information.
Classical information theory requires that any ``reasonable'' information can be expressed as a series of answers to yes-no questions, i.e. a string of bits. But unlike classical symbolic computation, where every single step of a computation can be mapped onto a bit-string, physical computation requires such a labeling only for the initial and the final machine state (see 2.1.3.2), the labels of which make up the input and output of the computation.
This requirement is in full accordance with the Copenhagen interpretation of quantum physics, which states that the setup and the outcome of any experiment has to be described in classical terms.
As the machine state ![]() is not directly accessible, any
physically realizable labeling has to correspond to an
observable
is not directly accessible, any
physically realizable labeling has to correspond to an
observable ![]() .
As has been shown in 1.3.2.2, in quantum physics,
an observable
.
As has been shown in 1.3.2.2, in quantum physics,
an observable ![]() is expressed by a Hermitian operator
is expressed by a Hermitian operator
![]() .
.
A natural choice for ![]() on an
on an ![]() -qubit quantum computer
would be the classical values
-qubit quantum computer
would be the classical values
![]() of the
singe qubits with the Hermitian operators
of the
singe qubits with the Hermitian operators
| (2.42) |
| (2.43) |
To set a quantum computer to a desired initial state
![]() corresponding to the boolean
input string
corresponding to the boolean
input string ![]() , it suffices to provide means to initially
``cool'' all qubits to
, it suffices to provide means to initially
``cool'' all qubits to ![]() and then apply any unitary
transformation
and then apply any unitary
transformation ![]() which matches the condition
which matches the condition
![]() .
.
As has been described in 1.3.2.3, it is impossible
to observe a quantum state ![]() without, at the same time,
forcing the system to adopt a state
without, at the same time,
forcing the system to adopt a state ![]() which is an
eigenstate of the Hermitian operator
which is an
eigenstate of the Hermitian operator ![]() corresponding to
the observed quantity
corresponding to
the observed quantity ![]() .
The transition probability is thereby given as
.
The transition probability is thereby given as
| (2.44) |
If we measure the binary values ![]() of an
of an ![]() -qubit
quantum computer in the state
-qubit
quantum computer in the state
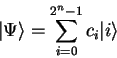 |
(2.45) |
| (2.46) |
Measurements don't have to cover the whole machine state, but can also be restricted to single qubits or quantum registers.
Consider two quantum registers with ![]() and
and ![]() qubits in the
state
qubits in the
state
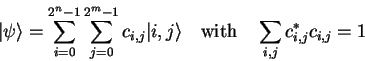 |
(2.47) |
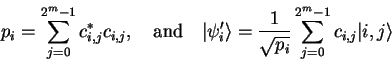 |
(2.48) |