


Next: Quantum Computers
Up: Quantum Physics in a
Previous: Wave Mechanics
Contents
Subsections
Algebraic Quantum Physics
While the Schrödinger Equation, in principle, allows to compute all
details of the particle distribution and the exact energy terms,
having to deal with partial differential equations, boundary conditions
and normalization factors, is usually very cumbersome and often
can't be done analytically, anyway.
Just a nobody would try to develop a color TV set by solving Maxwell
equations, the discussion of complex quantum systems requires a
more abstract formalism.
The solutions 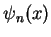 from the examples in section
1.2.3.3 and 1.2.3.4 are complex functions
over the intervals
from the examples in section
1.2.3.3 and 1.2.3.4 are complex functions
over the intervals
![${\mathcal{I}}=[0,l]$](img91.gif) or
or
![${\mathcal{I}}=[0,l]^3$](img92.gif) ,
respectively.
Let's introduce the following abbreviations1.8
,
respectively.
Let's introduce the following abbreviations1.8
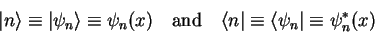 |
(1.24) |
or, for the case of 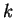 indices
indices
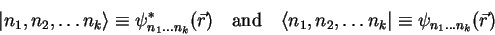 |
(1.25) |
and also introduce a scalar Product
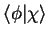 defined as
defined as
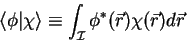 |
(1.26) |
The scalar product
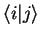 of the eigenfunctions
of the eigenfunctions 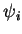 and
and 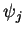 from the on dimensional capacitor example
(1.2.3.3) gives
from the on dimensional capacitor example
(1.2.3.3) gives
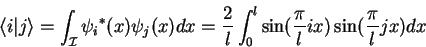 |
(1.27) |
The substitution
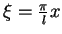 leads to
leads to
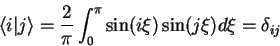 |
(1.28) |
So the eigenfunctions of the Hamilton operator 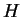 are
orthonormal according to the scalar product (1.26)
and therefor form the base of the orthonormal vector space
are
orthonormal according to the scalar product (1.26)
and therefor form the base of the orthonormal vector space
 consisting of all possible linear combinations
of
consisting of all possible linear combinations
of
 . This space is the Hilbert space
for this particular problem and it can be shown that the
eigenvalues of any operator describing a physical
observable form an orthogonal base.1.9
. This space is the Hilbert space
for this particular problem and it can be shown that the
eigenvalues of any operator describing a physical
observable form an orthogonal base.1.9
Completeness
Since the Schrödinger Equation is a linear differential equation,
any linear combination of solutions is also a solution and thus
a valid physical state.
To calculate the expectation value
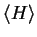 of the energy for a given
state
of the energy for a given
state 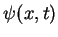 we have to solve the integral
we have to solve the integral
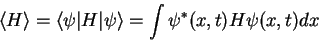 |
(1.29) |
If 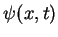 is given as a sum of eigenfunctions as in
equation 1.19, integration can be avoided, as
is given as a sum of eigenfunctions as in
equation 1.19, integration can be avoided, as
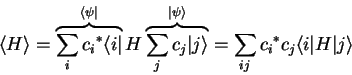 |
(1.30) |
Since
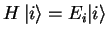 and
and
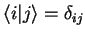 ,
,
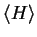 can be expressed as a weighted sum of eigenvalues:
can be expressed as a weighted sum of eigenvalues:
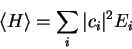 |
(1.31) |
Using the eigenfunctions for the one-dimensional capacitor (1.2.3.3)
the complex amplitudes 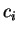 for an arbitrary continuous function
for an arbitrary continuous function 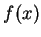 over
over ![$[0,l]$](img119.gif) are given by
are given by
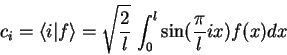 |
(1.32) |
This describes a standard sine-Fourier Transform.
The original function can be reconstructed by a composition
of eigenfunctions 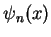 with the Fourier components
with the Fourier components
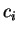
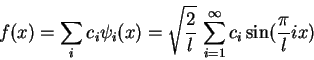 |
(1.33) |
As before, it can be shown that the eigenvalues of any Hamilton
operator always form a complete orthonormal base, thus
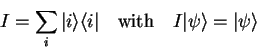 |
(1.34) |
A Hilbert space 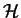 is a linear vector space over the
scalar body
is a linear vector space over the
scalar body 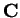 . Let
. Let
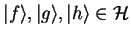 and
and
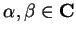 , then the following operations are
defined [23]:
, then the following operations are
defined [23]:
| |
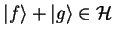 |
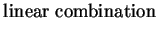 |
(1.35) |
| |
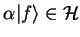 |
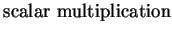 |
(1.36) |
| |
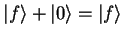 |
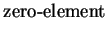 |
(1.37) |
| |
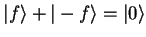 |
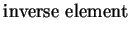 |
(1.38) |
The inner product
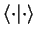 meets the following
conditions:
meets the following
conditions:
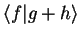 |
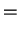 |
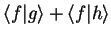 |
(1.39) |
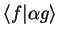 |
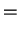 |
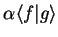 |
(1.40) |
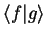 |
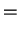 |
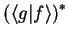 |
(1.41) |
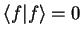 |
 |
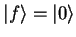 |
(1.42) |
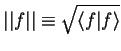 |
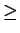 |
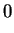 |
(1.43) |
As we have shown in 1.3.1.2, all valid states 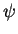 can
be expressed as a sum of eigenfunctions, i.e.
can
be expressed as a sum of eigenfunctions, i.e.
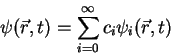 |
(1.44) |
If we use
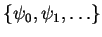 as unit vectors, we can
write the bra- and ket-vectors of
as unit vectors, we can
write the bra- and ket-vectors of 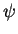 as infinitely
dimensional row- and column-vectors
as infinitely
dimensional row- and column-vectors
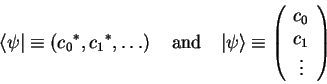 |
(1.45) |
The time independent Schrödinger equation can then be written as
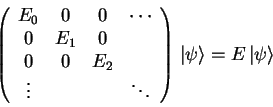 |
(1.46) |
The Hamilton Operator is the diagonal matrix
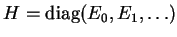 .
In the case of multiple
indices as in 1.2.3.4, a diagonalization such as e.g.
.
In the case of multiple
indices as in 1.2.3.4, a diagonalization such as e.g.
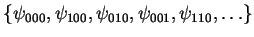 ,
can be used to order the eigenfunctions.
If such an diagonalization exists for a Hilbert space
,
can be used to order the eigenfunctions.
If such an diagonalization exists for a Hilbert space  , then every
linear operator
, then every
linear operator 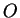 of
of 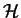 can be written in matrix form with
the matrix elements
can be written in matrix form with
the matrix elements
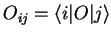 .
.
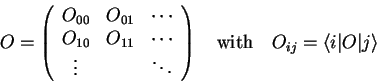 |
(1.47) |
Physical Observables
As has been mentioned in 1.2.2.3, in quantum physics, a physical
observable 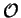 is expressed as a linear operator
is expressed as a linear operator 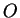 (see table 1.1)
while the classical value of
(see table 1.1)
while the classical value of 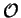 is the expectation value
is the expectation value
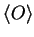 .
Obviously, the value of an observable such as position or momentum
must be real, as a length of
.
Obviously, the value of an observable such as position or momentum
must be real, as a length of
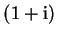 meter would have no physical meaning,
so we require
meter would have no physical meaning,
so we require
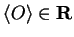 .
.
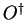 is called adjoint operator to
is called adjoint operator to 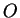 if
if
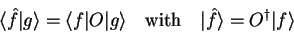 |
(1.48) |
If 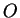 is given in matrix form, the
is given in matrix form, the 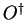 is the conjugated transposition
of
is the conjugated transposition
of 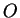 , i.e.
, i.e.
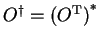 .
An operator
.
An operator 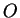 with
with
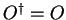 is called self adjoint
or Hermitian.
is called self adjoint
or Hermitian.
All quantum observables are represented by Hermitian operators as
we can reformulate the requirement
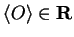 as
as
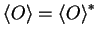 or
or
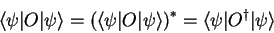 |
(1.49) |
Measurement
In classical physics, the observables of a system such as particle location,
momentum, Energy, etc. where thought to be well defined entities which
change their values over time according to certain dynamic laws and which could
-- technical difficulties aside -- in principle be observed without
disturbing the system itself.
It is a fundamental finding of quantum physics that this is not the case.
Consider a state
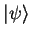 which is a composition of two eigenstates
which is a composition of two eigenstates
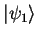 and
and
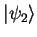 of the time-independent Schrödinger
equation with the assorted energy-eigenvalues
of the time-independent Schrödinger
equation with the assorted energy-eigenvalues 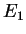 and
and 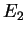
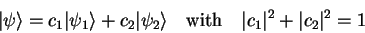 |
(1.52) |
The expectation value of energy
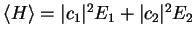 , but if
we actually perform the measurement, we will measure either
, but if
we actually perform the measurement, we will measure either 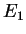 or
or
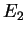 with the probabilities
with the probabilities 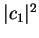 and
and 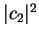 .
However, if we measure the resulting state again, we will always get the same
energy as in the first measurement as the wave function has
collapsed to either
.
However, if we measure the resulting state again, we will always get the same
energy as in the first measurement as the wave function has
collapsed to either 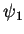 or
or 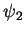 .
.
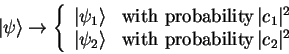 |
(1.53) |
The fact that
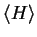 is only a statistical value, brings
up the question when it is reasonable to speak about the energy
of a state (or any other observable, for the matter) or,
with other words, whether a physical quality of a system exists
for itself or is invariably tied to the process of measuring.
is only a statistical value, brings
up the question when it is reasonable to speak about the energy
of a state (or any other observable, for the matter) or,
with other words, whether a physical quality of a system exists
for itself or is invariably tied to the process of measuring.
The Copenhagen interpretation of quantum physics argues
that an observable 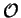 only exists if the system in
question happens to be in an eigenstate of the according
operator
only exists if the system in
question happens to be in an eigenstate of the according
operator 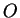 [22].
[22].
The destructive nature of measurement raises the question
whether 2 observables 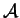 and
and 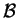 can
be measured simultaneously.
This can only be the case if the post-measurement state
can
be measured simultaneously.
This can only be the case if the post-measurement state 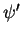 is an eigenfunction of
is an eigenfunction of 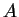 and
and 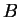
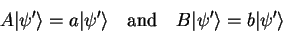 |
(1.54) |
Using the commutator ![$[A,B]=AB-BA$](img188.gif) , this is equivalent
to the condition
, this is equivalent
to the condition ![$[A,B]=0$](img189.gif) .
If
.
If 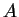 and
and 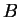 don't commute, then the uncertainty product
(see 1.2.2.3)
don't commute, then the uncertainty product
(see 1.2.2.3)
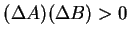 .
To find a lower limit for
.
To find a lower limit for
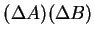 we introduce
the operators
we introduce
the operators
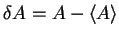 and
and
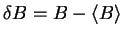 and can express the squared uncertainty product as
and can express the squared uncertainty product as
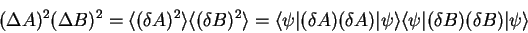 |
(1.55) |
Since 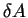 and
and 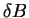 are self adjoint, we express
the above as
are self adjoint, we express
the above as
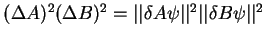 .
Using Schwarz's Inequality
.
Using Schwarz's Inequality
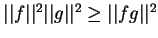 and
the fact that
and
the fact that
![$[A,B]=[\delta A,\delta B]$](img199.gif) we get
we get
![\begin{displaymath}
(\Delta A)(\Delta B) \ge \frac{1}{2} \vert\vert[A,B]\vert\vert
\end{displaymath}](img200.gif) |
(1.56) |
Observables with a nonzero commutator ![$[A,B]$](img201.gif) of the dimension
of action (i.e. a product of energy and time) are
canonically conjugated.
If we take e.g. the location and momentum operators from
1.2.2.3, we find that
of the dimension
of action (i.e. a product of energy and time) are
canonically conjugated.
If we take e.g. the location and momentum operators from
1.2.2.3, we find that
![\begin{displaymath}
(\Delta R_i)(\Delta P_j)\ge
\frac{1}{2}\vert\vert[r_i,-i\h...
...rtial }{\partial r_j}]\vert\vert=
\frac{1}{2}\hbar\delta_{ij}
\end{displaymath}](img202.gif) |
(1.57) |
This means that it is impossible to define the location and the
impulse for the same coordinate to arbitrary precision; it
is, however, possible the measure the location in 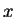 -direction
together with the impulse in
-direction
together with the impulse in 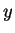 -direction.
-direction.
Temporal Evolution
In 1.2.3.1 we have shown how the Schrödinger
equation can be separated if the Hamilton operator is
time independent.
If we have the initial value problem with
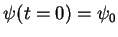 we can define an operator
we can define an operator 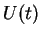 such that
such that
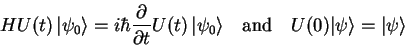 |
(1.58) |
We get the operator equation
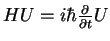 with the
solution
with the
solution
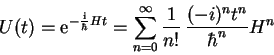 |
(1.59) |
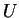 is the operator of temporal evolution and satisfies
the criterion
is the operator of temporal evolution and satisfies
the criterion
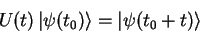 |
(1.60) |
If
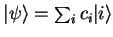 is a solution of the
time-independent Schrödinger equation, then
is a solution of the
time-independent Schrödinger equation, then
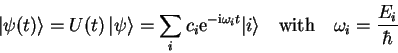 |
(1.61) |
is the corresponding time dependent solution
(see 1.2.3.1).
Unitary Operators
The operator of temporal evolution satisfies the condition
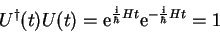 |
(1.62) |
Operators 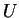 with
with
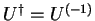 are called unitary.
Since the temporal evolution of a quantum system is described
by a unitary operator and
are called unitary.
Since the temporal evolution of a quantum system is described
by a unitary operator and
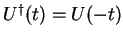 it follows that
the temporal behavior of a quantum system is reversible,
as long a no measurement is performed.1.10
it follows that
the temporal behavior of a quantum system is reversible,
as long a no measurement is performed.1.10
Unitary operators can also be used to describe abstract operations
like rotations
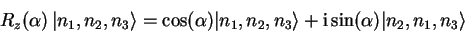 |
(1.63) |
or the flipping of eigenstates
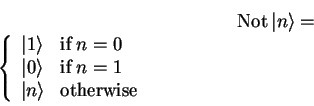 |
(1.64) |
without the need to specify how this transformations are actually
performed or having to deal with time-dependent Hamilton operators.
Mathematically, unitary operations can be described as
base-transformations between 2 orthonormal bases (just like
rotations in 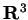 ).
Let
).
Let 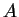 and
and 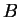 be Hermitian operators with the orthonormal
eigenfunctions
be Hermitian operators with the orthonormal
eigenfunctions 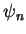 and
and
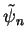 and
and
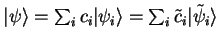 , then the Fourier
coefficients
, then the Fourier
coefficients 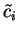 are given by
are given by
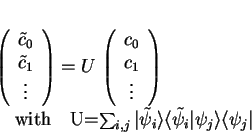 |
(1.65) |
In section 1.2.3.4 we have calculated the eigenstates
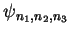 for an electron in a 3 dimensional trap.
Real electrons are also characterized by the orientation of
their spin which can be either ``up'' (
for an electron in a 3 dimensional trap.
Real electrons are also characterized by the orientation of
their spin which can be either ``up'' ( ) or
``down'' (
) or
``down'' ( ). The spin-state
). The spin-state
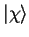 of an
electron can therefor be written as
of an
electron can therefor be written as
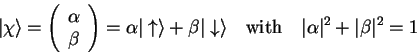 |
(1.66) |
The spins also form a finite Hilbert space
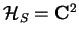 with the orthonormal base
with the orthonormal base
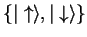 .
If we combine
.
If we combine 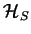 with the solution space
with the solution space 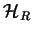 for
the spinless problem (equation 1.22), we get a combined
Hilbert space
for
the spinless problem (equation 1.22), we get a combined
Hilbert space
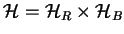 with the base-vectors
with the base-vectors
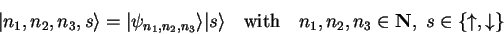 |
(1.67) |
Product States
If we have two independent quantum systems A and B described by
the Hamilton operators 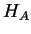 and
and 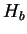 with the orthonormal
eigenvectors
with the orthonormal
eigenvectors 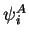 and
and 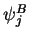 , which are in the
states
, which are in the
states
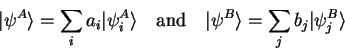 |
(1.68) |
then the common state
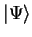 is given by
is given by
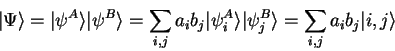 |
(1.69) |
Such states are called product states.
Unitary transformations and measurements applied
to only one subsystem don't affect the other as
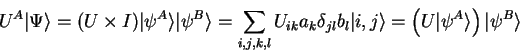 |
(1.70) |
and the probability 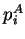 to measure the energy
to measure the energy
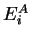 in system A is given by1.11
in system A is given by1.11
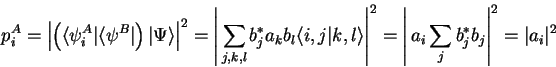 |
(1.71) |
If
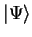 is not a product state, then operations
on one subsystem can affect the other.
Consider two electrons with the common spin state
is not a product state, then operations
on one subsystem can affect the other.
Consider two electrons with the common spin state
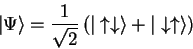 |
(1.72) |
If we measure the spin of the first electron, we get either
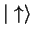 or
or
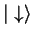 with the equal
probability
with the equal
probability 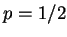 which the resulting post-measurement states
which the resulting post-measurement states
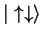 or
or
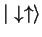 .
Consequently, if we measure the spin of the second electron, we
will always find it to be anti-parallel to the first.
.
Consequently, if we measure the spin of the second electron, we
will always find it to be anti-parallel to the first.
Two systems whose common wave-function
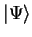 is not
a product state are entangled.
is not
a product state are entangled.
Footnotes
- ... abbreviations1.8
-
This formalism is called Braket notation and has been
introduced by Dirac: The
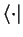 terms are referred to as
``bra''- and the
terms are referred to as
``bra''- and the
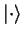 terms as ``ket''-vectors.
terms as ``ket''-vectors.
- ... base.1.9
- As physical
observables are real values, their corresponding operators
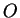 have to be self-adjoint i.e.
have to be self-adjoint i.e.
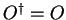
- ... performed.1.10
- since a measurement
can result in a reduction of the wave-function (see
1.3.2.3), it is generally impossible to reconstruct
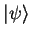 from the post-measurement state
from the post-measurement state
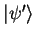
- ... by1.11
- We assume here
that the eigenvalue
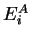 isn't degenerated, otherwise
the solution is analog to equation 1.50.
isn't degenerated, otherwise
the solution is analog to equation 1.50.



Next: Quantum Computers
Up: Quantum Physics in a
Previous: Wave Mechanics
Contents
(c) Bernhard Ömer - oemer@tph.tuwien.ac.at - http://tph.tuwien.ac.at/~oemer/
![]() from the examples in section
1.2.3.3 and 1.2.3.4 are complex functions
over the intervals
from the examples in section
1.2.3.3 and 1.2.3.4 are complex functions
over the intervals
![]() or
or
![]() ,
respectively.
Let's introduce the following abbreviations1.8
,
respectively.
Let's introduce the following abbreviations1.8
![]() of the energy for a given
state
of the energy for a given
state ![]() we have to solve the integral
we have to solve the integral
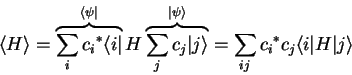
![]() is a linear vector space over the
scalar body
is a linear vector space over the
scalar body ![]() . Let
. Let
![]() and
and
![]() , then the following operations are
defined [23]:
, then the following operations are
defined [23]:
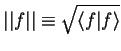
![]() can
be expressed as a sum of eigenfunctions, i.e.
can
be expressed as a sum of eigenfunctions, i.e.
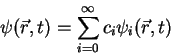
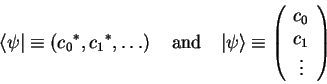
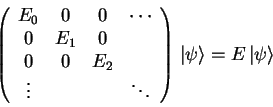
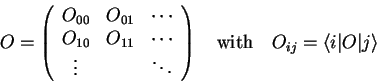
![]() is expressed as a linear operator
is expressed as a linear operator ![]() (see table 1.1)
while the classical value of
(see table 1.1)
while the classical value of ![]() is the expectation value
is the expectation value
![]() .
Obviously, the value of an observable such as position or momentum
must be real, as a length of
.
Obviously, the value of an observable such as position or momentum
must be real, as a length of
![]() meter would have no physical meaning,
so we require
meter would have no physical meaning,
so we require
![]() .
.
![]() is called adjoint operator to
is called adjoint operator to ![]() if
if
![]() as
as
![]() or
or
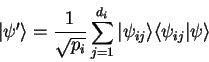
![]() which is a composition of two eigenstates
which is a composition of two eigenstates
![]() and
and
![]() of the time-independent Schrödinger
equation with the assorted energy-eigenvalues
of the time-independent Schrödinger
equation with the assorted energy-eigenvalues ![]() and
and ![]()
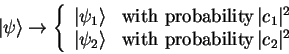
![]() is only a statistical value, brings
up the question when it is reasonable to speak about the energy
of a state (or any other observable, for the matter) or,
with other words, whether a physical quality of a system exists
for itself or is invariably tied to the process of measuring.
is only a statistical value, brings
up the question when it is reasonable to speak about the energy
of a state (or any other observable, for the matter) or,
with other words, whether a physical quality of a system exists
for itself or is invariably tied to the process of measuring.
![]() only exists if the system in
question happens to be in an eigenstate of the according
operator
only exists if the system in
question happens to be in an eigenstate of the according
operator ![]() [22].
[22].
![]() and
and ![]() can
be measured simultaneously.
This can only be the case if the post-measurement state
can
be measured simultaneously.
This can only be the case if the post-measurement state ![]() is an eigenfunction of
is an eigenfunction of ![]() and
and ![]()
![\begin{displaymath}
(\Delta R_i)(\Delta P_j)\ge
\frac{1}{2}\vert\vert[r_i,-i\h...
...rtial }{\partial r_j}]\vert\vert=
\frac{1}{2}\hbar\delta_{ij}
\end{displaymath}](img202.gif)
![]() we can define an operator
we can define an operator ![]() such that
such that
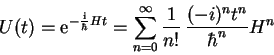
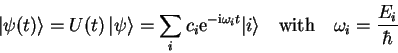
![]() ).
Let
).
Let ![]() and
and ![]() be Hermitian operators with the orthonormal
eigenfunctions
be Hermitian operators with the orthonormal
eigenfunctions ![]() and
and
![]() and
and
![]() , then the Fourier
coefficients
, then the Fourier
coefficients ![]() are given by
are given by
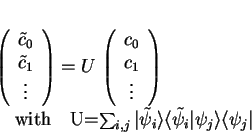
![]() for an electron in a 3 dimensional trap.
Real electrons are also characterized by the orientation of
their spin which can be either ``up'' (
for an electron in a 3 dimensional trap.
Real electrons are also characterized by the orientation of
their spin which can be either ``up'' (![]() ) or
``down'' (
) or
``down'' (![]() ). The spin-state
). The spin-state
![]() of an
electron can therefor be written as
of an
electron can therefor be written as
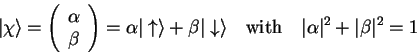
![]() and
and ![]() with the orthonormal
eigenvectors
with the orthonormal
eigenvectors ![]() and
and ![]() , which are in the
states
, which are in the
states
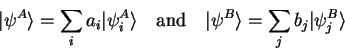
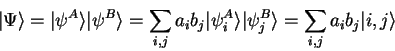
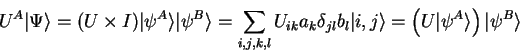
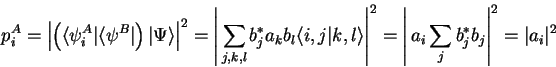
![]() is not a product state, then operations
on one subsystem can affect the other.
Consider two electrons with the common spin state
is not a product state, then operations
on one subsystem can affect the other.
Consider two electrons with the common spin state
![]() is not
a product state are entangled.
is not
a product state are entangled.