In classical physics, the momentary state of a particle is given by
it's location ![]() and it's velocity
and it's velocity ![]() .
.
When we talk about the temporal behavior of dynamic systems, however, this notion of ``state'' is somewhat cumbersome to deal with, since by definition, the momentary state of the system changes constantly. This is especially true when it comes to periodic movement, so it is often more adequate to talk about the current orbit of a satellite (which remains constant until it is actively altered by outside intervention) than to give the actual coordinates (which permanently change).
So in a more abstract definition, the states of an isolated classical
system are the positions
![]() of all included
particles as a function of time
of all included
particles as a function of time ![]() .1.2
.1.2
The above definition implies that the state of a system can only change when an interaction with another system occurs.
Typically, the duration of the interaction (e.g. the collision of 2 billiard-balls) is very small compared to the duration of the isolated states, so for practical purposes the interaction can often be assumed as instantaneous.
Isolated systems preserve their total energy ![]() and momentum1.3
and momentum1.3 ![]() ,
which are given as1.4
,
which are given as1.4
| (1.4) |
Legal physical states must obey a movement law which characterizes
the dynamics of a system. For classic one-particle systems, the
dynamic equation is known as Newton's Second Law
| (1.5) |
In quantum physics, the state of a one-particle system is
characterized by a complex distribution function
![]() with the normalization
with the normalization
| (1.7) |
Two states differing by a constant phase factor
![]() are considered equivalent.
are considered equivalent.
The classical notion of particle location is replaced by a
spatial probability distribution
![]() ,
which can be characterized by its expectation value
,
which can be characterized by its expectation value
![]() and its uncertainty
and its uncertainty ![]() , which are
defined as
, which are
defined as
| (1.8) |
When a classical system involves moving particles, the location
of the particles is time dependent. This is not necessarily the
case with quantum systems and the describing probability distribution
![]() :
If the quantum state
:
If the quantum state ![]() is of the form
is of the form
![]() with
with ![]() ,
then
,
then
![]() is time independent.
is time independent.
Figure 1.1 shows a particle that is trapped between two reflecting ``mirrors''.1.5A classical particle will move periodically from on end to another at a constant speed, it's location can be described by a periodic triangle-function of the time. An undisturbed quantum particle in a similar trap, however, doesn't have a defined location; the probability to ``meet'' (i.e. measure) the particle at a certain location remains constant over time1.6but changes throughout space, or in more physical terms, the particle forms a standing wave just as a vibrating piano-string between 2 fixed ends.
A constant probability distribution is typical for bound states of defined energy, i.e. for particles trapped in a constant potential well, e.g. an electron in the electric field of a proton.
It has been shown above how the classical concept of a well defined particle location has been replaced by the quantum concept of a statistical expectation value. This correspondence, however, is not just restricted to space. In fact, all classical physical quantities of a system can be described as the expectation value of an appropriate operator (see table 1.1 for some examples).
In analogy to equation 1.2.2.1, the expectation value
![]() and the
uncertainty for an observable
and the
uncertainty for an observable ![]() are defined as
are defined as
| (1.9) |
The quantum analogy to Newton's Third Law (see equation 1.6)
is the Schrödinger Equation
If we take the simple case of a particle in a static
potential field ![]() , equation 1.10 can be written as
, equation 1.10 can be written as
| (1.13) |
The remaining eigenvalue problem
![]() is
also called the time-independent Schrödinger Equation.1.7
is
also called the time-independent Schrödinger Equation.1.7
Depending on the imposed boundary conditions, the Schrödinger
Equation is often only solvable for particular values of ![]() ,
i.e. it has a discrete energy spectrum and the possible
eigenvalues
,
i.e. it has a discrete energy spectrum and the possible
eigenvalues ![]() (also called energy terms) can be enumerated.
The solution for the lowest eigenvalue
(also called energy terms) can be enumerated.
The solution for the lowest eigenvalue ![]() is called the ground-state
is called the ground-state
![]() of the system.
of the system.
Since for most physical applications, only the value of the energy terms is of importance, it is hardly ever necessary to actually compute the eigenstates.
It has been the discovery of discrete energy states, which gave quantum
physics its name, as any state change from eigenstate ![]() to
to
![]() involves the exchange of an energy quantum
involves the exchange of an energy quantum
![]() .
.
As an example, let's consider an electron in a capacitor. To keep
things simple, the capacitor should be modeled by an infinitely
deep, one-dimensional potential well (see also 1.2.2.2),
thus
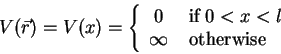 |
(1.14) |
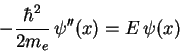 |
(1.15) |
| (1.16) |
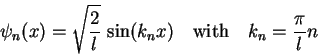 |
(1.17) |
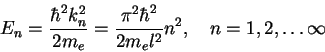 |
(1.18) |
Figure 1.2 shows the first 3 eigenstates
![]() and
and ![]() and their corresponding spatial probability distributions
and their corresponding spatial probability distributions
![]() .
.
The above example can easily be extended to 3 dimensions, using the
potential
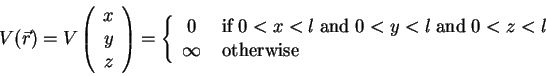 |
(1.21) |
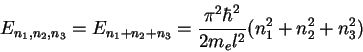 |
(1.23) |