An important problem in physics before the adoption of the quantum theory, has been the distinction between particle and wave phenomena.
At first glance, both concepts have very little in common: Nobody would treat a flying bullet as a wave packet or the propagation of sound as a particle stream, but when particles and wave-lengths get smaller, things aren't so clear:
In the ![]() century, Newton used both theories to cover
the different aspects of light [23], explaining
its periodicy and interference as wave, and it's linear propagation
as particle phenomenon.
Later, the wave-theory of light has been generally accepted, as
scientists like Young and Fresnel could explain most particulate
behavior within the realm of the wave-formalism.
Except, that is, for one fundamental requirement: The obvious lack of a
physical medium which lead to the somewhat far-fetched and
unsatisfying ``Ether'' hypothesis.
century, Newton used both theories to cover
the different aspects of light [23], explaining
its periodicy and interference as wave, and it's linear propagation
as particle phenomenon.
Later, the wave-theory of light has been generally accepted, as
scientists like Young and Fresnel could explain most particulate
behavior within the realm of the wave-formalism.
Except, that is, for one fundamental requirement: The obvious lack of a
physical medium which lead to the somewhat far-fetched and
unsatisfying ``Ether'' hypothesis.
On the particle front, Dalton's Law of Multiple Proportions suggested,
that chemical substances consist of atoms of different masses.
In the ![]() century, Boltzmann developed his gas-theory based
on atomistic concepts and experiments with cathode rays showed that the electric
charges always come in multiples of the elementary charge e which is
about
century, Boltzmann developed his gas-theory based
on atomistic concepts and experiments with cathode rays showed that the electric
charges always come in multiples of the elementary charge e which is
about
![]() Coulomb.
Coulomb.
In the year 1900, Max Plank explained the energy spectrum of
black body radiation with the ad-hoc assumption, that the
possible energy states are restricted to ![]() , where
, where
![]() is an integer,
is an integer, ![]() the frequency and
the frequency and ![]() the Plank
constant, the fundamental constant of quantum physics, with
a value of
the Plank
constant, the fundamental constant of quantum physics, with
a value of
In 1888, Hertz demonstrated, that a negatively charged plate would discharge, if exposed to ultraviolet light. Lenard later discovered the kinetic energy of the electrons is independent of the light's intensity but correlated to its frequency, such that
with some material dependent constant ![]() . In 1905 Einstein
reformulated this relation to
. In 1905 Einstein
reformulated this relation to
interpreting ![]() as the energy of a light particle, later called
a photon.
as the energy of a light particle, later called
a photon.
By analyzing the visible spectrum of Hydrogen, it was found
that the light intensity shows very distinct peaks at certain
wavelengths.
In 1885, Balmer showed that the wavelength ![]() is very accurately
given by
is very accurately
given by
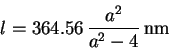 |
(1.1) |
| (1.2) |
The Bohr-Sommerfeld model accounted for this by introducing a
quantum condition: While the electrons are still assumed to circulate
the nucleus on their classical orbits, their angular momentum
has to be a multiple of ![]() .
This restriction could be justified by attributing wave properties
to the electron and demanding that their corresponding wave functions
form a standing wave; however this kind of hybrid theory remained
unsatisfactory.
.
This restriction could be justified by attributing wave properties
to the electron and demanding that their corresponding wave functions
form a standing wave; however this kind of hybrid theory remained
unsatisfactory.
A complete solution for the problem came in 1923 from Heisenberg who used a matrices-based formalism. In 1925, Schrödinger published an alternative solution using complex wave functions. It took two years until Dirac showed that both formalisms were in fact equivalent.
In 1924, de Broglie assumed that -- in analogy to photons -- every
particle of energy ![]() and momentum
and momentum ![]() can in fact be treated as
a wave, whose frequency
can in fact be treated as
a wave, whose frequency ![]() and wave-vector
and wave-vector ![]() are
given by
are
given by
| (1.3) |