As pointed out in 3.1.3, any quantum computation must be a composition of initializations, unitary operators and measurements. A typical probabilistic quantum algorithm usually runs an evaluation loop like this:
{
reset; // R: |Psi> -> |0>
myoperator(q); // U: |0> -> |Psi'>
measure q,m; // M: |Psi'> -> |m>
} until ok(m); // picked the right m ?
|
The reset command resets the machine-state
![]() to
to ![]() , which is also the initial state when
qcl is started.
The quantum heap and the binding of quantum variables are
unaffected.
, which is also the initial state when
qcl is started.
The quantum heap and the binding of quantum variables are
unaffected.
The outcome of the measurement is determined by a random number generator, which -- by default -- is initialized with the current system time. For reproducible behavior of the simulation, a seed value can be given with the option -seed.
Since reset and measure operations are irreversible, they must not occur within operator definitions.
Besides the classical subroutine type procedure and function, QCL provides two quantum routine types for general unitary operators (operator) and pseudo-classic operators (qufunct). QCL allows to invert operators and can perform scratch-space management for quantum functions, thus allowed side effects on the classical program state as well as on the quantum machine state have to be strictly specified.
The 4 QCL routine types form a call hierarchy, which means that a routine may invoke only subroutines of the same or a lower level (see table 3.6).
The mathematical semantic of QCL operators and functions requires that every call is reproducible. This means, that not only the program state must not be changed by these routines, but also that their execution may in no way depend on the global program state which includes global variables, options and the state of the internal random number generator.
While QCL incorporates a classical programming language, to provides all the necessary means to change the program state, there is no hardwired set of elementary operators to manipulate the quantum machine state, since this would require assumptions about the architecture of the simulated quantum computer.
An elementary operator or qufunct can be incorporated by declaring it as extern.

Section 3.4.4 and 3.4.7 describe the elementary unitary and pseudo classic gates which are provided by the integrated simulator of qcl.
The routine type operator is used for general unitary operators. Conforming to the mathematical notion of an operator, a call with the same parameters has to result in exactly the same transformation, so no global variable references, random elements or dependencies on input are allowed.
Since the type operator is restricted to reversible transformations of the machine state, reset and measure commands are also forbidden.
Operators work on one or more quantum registers
so a call of an ![]() qubit operator with a total quantum
heap of
qubit operator with a total quantum
heap of ![]() qubits can result in
qubits can result in
![]() different unitary transformations.
different unitary transformations.
In QCL, this polymorphism is even further extended by
the fact, that quantum registers can be of different
sizes, so for every quantum parameter ![]() , the
register size
, the
register size
![]() is an
implicit extra parameter of type int.
An addition to that, operators can take an arbitrary number
of explicit classical arguments.
is an
implicit extra parameter of type int.
An addition to that, operators can take an arbitrary number
of explicit classical arguments.
If more than one argument register is given, their qubits may not overlap.
qcl> qureg q[4]; qcl> qureg p=q[2:3]; qcl> CNot(q[1\2],p); ! runtime error: quantum arguments overlapping |
Operator calls
can be inverted by the adjungation prefix `!'.
The adjoint operator to a composition of unitary operators
is3.3
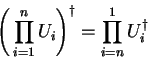 |
(3.15) |
When the adjungation flag is set, the operator body is executed and all calls of suboperators are pushed on a stack which is then processed in reverse order with inverted adjungation flags.
As opposed to pseudo-classic operators, it is in general
impossible to uncompute a unitary operator in order
to free a local register again without also destroying
the intended result of the computation.
This is a fundamental limitation of QC known as the non
cloning theorem which results from the fact that a
cloning operation i.e. a transformation with meets the condition
| (3.16) |
| (3.17) | |||
| (3.18) |
Due to the lack of a unitary copy operation for quantum states, Bennet-style scratch space management is impossible for general operators since it is based on cloning the result register.
Despite this limitation, it is possible in QCL to allocate temporary quantum registers but it is up to the programmer to properly uncompute them again. If the option -check is set, proper cleanup is verified by the simulator.
qcl> set check 1
qcl> operator foo(qureg q) { qureg p[1]; CNot(p,q); }
qcl> qureg q[1];
qcl> Mix(q);
[1/4] 0.707107 |0000> + 0.707107 |0001>
qcl> foo(q);
! in operator foo: memory error: quantum heap is corrupted
[1/4] 0.707107 |0000> + 0.707107 |0011>
|
The most general form for specifying a unitary operator
(or any other linear transformation) is by defining it's
matrix elements:
An ![]() qubit unitary operator
qubit unitary operator ![]() describes a transformation
describes a transformation
![]() and therefore corresponds to
a
and therefore corresponds to
a
![]() matrix in
matrix in ![]()
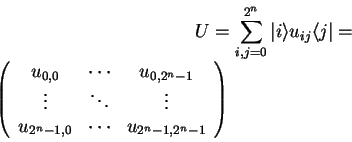 |
(3.19) |
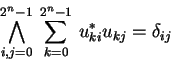 |
(3.20) |
extern operator Matrix2x2( complex u00,complex u01, complex u10,complex u11, qureg q); extern operator Matrix4x4(...,qureg q); extern operator Matrix8x8(...,qureg q); |
qcl> const i=(0,1); qcl> qureg q[1]; qcl> Matrix2x2(i*cos(pi/6),i*sin(pi/6),(0,0),(1,0),q); ! external error: matrix operator is not unitary |
The rotation of a single qubit is defined by the
transformation matrix ![]()
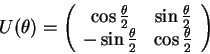 |
(3.21) |
extern operator Rot(real theta,qureg q); |
qcl> Rot(pi/2,q); ! external error: Only single qubits can be rotated |
The Hadamard Gate is a special case of a generalized
qubit Rotation and defined by the transformation matrix ![]()
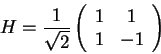 |
(3.22) |
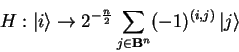 |
(3.23) |
The Hadamard Transformation is self adjoint (i.e.
![]() ),
which, for unitary operators, implies that
),
which, for unitary operators, implies that ![]() .
.
Since ![]() only contains uniform superpositions
that just differ by the signs of the base-vectors,
the external implementation of
only contains uniform superpositions
that just differ by the signs of the base-vectors,
the external implementation of ![]() is called
is called ![]() .
.
extern operator Mix(qureg q); |
The conditional phase gate is a pathological case
of a conditional operator (see 2.2.2.6), for
the zero-qubit phase operator
![]() .
.
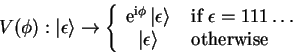 |
(3.24) |
extern operator CPhase(real phi,qureg q); |
The routine type qufunct is used for pseudo-classic
operators and quantum functions, so all transformations
have to be of the form
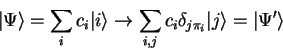 |
(3.25) |
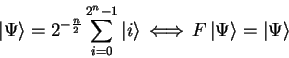 |
(3.26) |
The most straightforward application for pseudo-classic operators is the direct implementation of bijective functions (see 2.2.2.4)
qufunct inc(qureg x) {
int i;
for i = #x-1 to 1 {
CNot(x[i],x[0:i-1]);
}
Not(x[0]);
}
|
qcl> qureg q[4]; qcl> inc(q); [4/4] 1 |0001> qcl> inc(q); [4/4] 1 |0010> qcl> inc(q); [4/4] 1 |0011> qcl> inc(q); [4/4] 1 |0100> |
When it comes to more complicated arithmetic operations,
it is often required to apply a transformation to a
register ![]() in dependence on the content of
another register
in dependence on the content of
another register ![]() .
.
If all qubits of ![]() are required to be set,
for the transformation to take place, the operator
is a conditional operator with the invariant (quconst)
enable register
are required to be set,
for the transformation to take place, the operator
is a conditional operator with the invariant (quconst)
enable register ![]() (see 2.2.2.6).
(see 2.2.2.6).
A simple example for a conditional operator is the
Toffoli gate
| (3.27) |
qufunct cinc(qureg x,quconst e) {
int i;
for i = #x-1 to 1 step -1 {
CNot(x[i],x[0:i-1] & e);
}
CNot(x[0],e);
}
|
qcl> qureg q[4]; qureg e[2]; Mix(e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110000> qcl> cinc(q,e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110001> qcl> cinc(q,e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110010> qcl> cinc(q,e); [6/6] 0.5 |000000> + 0.5 |100000> + 0.5 |010000> + 0.5 |110011> |
As defined in 2.2.2.5, a quantum function ![]() is a
pseudo-classic operator with the characteristic
is a
pseudo-classic operator with the characteristic
| (3.28) |
Since, according to the above definition, quantum functions are merely ordinary pseudo-classic operators, whose specification is restricted to certain types of input states, they also use the same QCL routine type qufunct.
The following example calculates the parity of ![]() and stores it to
and stores it to ![]() :
:
qufunct parity(quconst x,quvoid y) {
int i;
for i = 0 to #x-1 {
CNot(y,x[i]);
}
}
qcl> qureg x[2]; qureg y[1]; Mix(x);
[3/3] 0.5 |000> + 0.5 |010> + 0.5 |001> + 0.5 |011>
qcl> parity(x,y);
[3/3] 0.5 |000> + 0.5 |110> + 0.5 |101> + 0.5 |011>
|
We can extend the notion of quantum functions, by also
allowing an explicit scratch register ![]() (see 3.3.2.4)
as an optional parameter to
(see 3.3.2.4)
as an optional parameter to ![]() , so we end up with an
operator
, so we end up with an
operator
![]() with the
characteristic
with the
characteristic
| (3.29) |
qufunct addparity(quconst x,quvoid y,quscratch s) {
parity(x,s); // write parity to scratch
x -> y; // Fanout x to y
cinc(y,s); // increment y if parity is odd
parity(x,s); // clear scratch
}
qcl2> qureg x[2]; qureg y[2]; qureg s[1]; Mix(x);
[5/8] 0.5 |00000> + 0.5 |00010> + 0.5 |00001> + 0.5 |00011>
qcl2> addparity(x,y,s);
[5/8] 0.5 |00000> + 0.5 |01110> + 0.5 |01001> + 0.5 |01111>
|
qufunct addparity2(quconst x,quvoid y) {
qureg s[1];
parity(x,s);
x -> y;
cinc(y,s);
parity(x,s);
}
qcl2> qureg x[2]; qureg y[2]; Mix(x);
[4/8] 0.5 |00000> + 0.5 |00010> + 0.5 |00001> + 0.5 |00011>
qcl2> addparity2(x,y);
[4/8] 0.5 |00000> + 0.5 |01110> + 0.5 |01001> + 0.5 |01111>
|
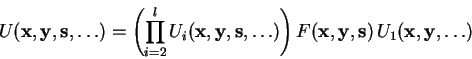 |
(3.30) |
| (3.31) |
The most general form for specifying an ![]() qubit pseudo-classic
operator
qubit pseudo-classic
operator ![]() , is by explicitly defining the underlying
permutation
, is by explicitly defining the underlying
permutation ![]() of base-vectors:
of base-vectors:
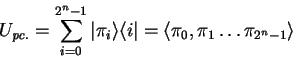 |
(3.32) |
QCL provides external operators for vector permutations
for ![]() , 4, 8, 16, 32 and 64 which the programmer
can use to directly implement a custom set of
, 4, 8, 16, 32 and 64 which the programmer
can use to directly implement a custom set of ![]() to
to
![]() qubit pseudo-classical operators:
qubit pseudo-classical operators:
extern qufunct Perm2(int p0 ,int p1 ,qureg q); extern qufunct Perm4(int p0 ,int p1 ,int p2 ,int p3 ,qureg q); extern qufunct Perm8(...,qureg q); extern qufunct Perm16(...,qureg q); extern qufunct Perm32(...,qureg q); extern qufunct Perm64(...,qureg q); |
qcl> qureg q[3]; qcl> Perm8(0,0,1,2,3,4,5,6,q); ! external error: no permutation |
The
![]() operation is a quantum function
(see 2.2.2.5)
and stands for a class of transformations with the
characteristic
operation is a quantum function
(see 2.2.2.5)
and stands for a class of transformations with the
characteristic
![]()
The external fanout operator of QCL is defined as
| (3.33) |
extern qufunct Fanout(quconst a,quvoid b); |
The ![]() operator exchanges the qubits of two equal
sized registers (
operator exchanges the qubits of two equal
sized registers (
![]() ).
A one to one qubit
).
A one to one qubit ![]() operator has the transformation
matrix
operator has the transformation
matrix
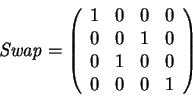 |
(3.34) |
extern qufunct Swap(qureg a,qureg b); |
The not operator ![]() inverts a qubit. Its transformation
matrix is
inverts a qubit. Its transformation
matrix is
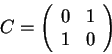 |
(3.35) |
![\begin{displaymath}
C_{[[\mathbf{e}]]}:{\vert b \rangle}{\vert\epsilon \rangle}...
...\rangle}_\mathbf{e} & \;\mbox{otherwise}
\end{array}\right.\end{displaymath}](img603.gif) |
(3.36) |
extern qufunct Not(qureg q); extern qufunct CNot(qureg q,quconst c); |
qcl> qureg q[4]; qureg p[4]; qcl> Not(q); [8/8] 1 |00001111> qcl> CNot(p,q); [8/8] 1 |11111111> |