Filtern ( wflt)

	Syntax: `wflt` [ options ] [ $\langle$ wave-file $\rangle$ ]

Options:	`-m` $\langle$ width $\rangle$	:	Mittelwertfilter
	`-l` $\langle$ frequency $\rangle$	:	Tiefpaßfilter
	`-f` $\langle$ frequency $\rangle$	:	Hochpaßfilter
	`-b` $\langle$ frequency $\rangle$	:	Bandpaßfilter
	`-w` $\langle$ frequency $\rangle$	:	Breite des Bandpasses (nur mit Opt. `-b`)
	`-g` $\langle$ gain $\rangle$	:	Verstärkung
	`-a` $\langle$ bias $\rangle$	:	Verschiebung des Nullpunktes
	`-c`	:	Zentrieren der erzeugeten Datei
	`-n`	:	Normalisieren der erzeugten Datei
	`-r`	:	Datei verkehrt abspielen
	`-i`	:	Datei invertieren

wflt ermöglicht eine breite Palette von beliebig kombinierbaren Transformationen, die in der oben angeführten Reihenfolge angewendet werden. Alle Frequenzangaben sowie die Angabe der Breite des Mittelwertfilters können direkt als Frequenz in Hz, als Periodendauer in s, oder als Anzahl der Sample-Werte, die einer Periode entsprechen (keine Einheit), angegeben werden. Für eine Datei mit einer Sample-Frequenz von 11025 Hz sind demnach die Frequenz-Parameter 2205Hz, 0.4531ms und 5 äquivalent.

In den folgenden Funktionsbeschreibungen stellt

immer die Datei vor, und

die Datei nach der jeweiligen Transformation dar. Indizes beziehen sich auf die jeweilige Fileposition (

entspricht demnach dem

-ten Sample-Wert). Der Differenz-Operator $\Delta$ sei definiert als $\Delta x = x_i - x_{i-1}$ . Weiters seien

bzw. $\omega_s = 2 \pi f_s$ und $T_s = {1\over f_s}$ Sampling-Frequenz bzw. Kreisfrequenz und Tastperiode.

Frequenzfilter

Mit Ausnahme des Mittelwertfilters sind alle implementierten Frequenzfilter (Optionen -l, -f und -b) den jeweiligen elektronischen Grundschaltungen (RC, RL und RCL-Glied) nachempfunden und als Differenzengleichungen mittels Rekursion implementiert. Um die Genauigkeit zu erhöhen und um bei Filterfrequenzen größer als $f_s\over 2 \pi$ ein Überschwingen zu vermeiden, wird $\Delta t = {4\over f_s}$ als Schrittweite verwendet und zwischen zwei Sample-Werten linear interpoliert. Nichtsdestoweniger bleiben Filterfrequenzen größer als ${1\over 2}f_s$ sinnlos, da diese nicht mehr darstellbar sind (Digitalisierungsrauschen).

In Tabelle 2.5.1 sind die mathematischen Definitionen der einzelnen Filter sowie ihre Diskretisierungen angegeben. $f_0 = {1\over t_0} = {f_s \over n} = {\omega_0 \over 2 \pi}$ steht dabei für die jeweilige Filterfrequenz. Im Falle des Bandpasses ( -b) gibt $w = {\Gamma \over 2 \pi}$ die Breite des Bandpasses an; ist diese nicht mit der Option -w angegeben so wird sie standardmäßig auf $w = {1\over 2} f_0$ gesetzt. 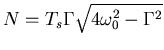Der Wert der Normierungskonstante $N = T_s \Gamma \sqrt{4 \omega_0^2-\Gamma^2}$ ist so gewählt, daß die maximale Verstärkung einer Sinus-Schwingung genau 1 ergibt. Anfangswerte (

) und undefinierte Randwerte (z.B. $x_{-1}$ ) sind auf 0 gesetzt.

**Abbildung 6:** **Frequenzfilter**
$\begin{figure}\small\centerline {\fbox{ $\begin{array}{l @{\hspace{3mm}} l @{\;\... ...ma \, \Delta \, y - T_s^2 \omega_0^2 y + N \, x \end{array}$}}\small\end{figure}$

Die folgenden Aufrufe wenden jeden der vier Filter auf die Datei Impuls.wav aus Abb. 4 an. Abb. 7 - 10 zeigen die Ausgaben der Aufrufe.

**Abbildung 7:** **Mittelwertfilter 1 kHz**
**Abbildung:** **Tiefpaß 200 Hz**
$\begin{figure} \hfill \parbox {70mm}{\centerline{\fbox{\epsffile{Meanvalue.ps}... ...x {70mm}{\centerline{\fbox{\epsffile{Lowpass.ps}}} \small} \hfill \end{figure}$

**Abbildung:** **Hochpaß 200 Hz**
**Abbildung:** **Bandpaß 200 Hz**
$\begin{figure} \hfill \parbox {70mm}{\centerline{\fbox{\epsffile{Highpass.ps}}... ... {70mm}{\centerline{\fbox{\epsffile{Bandpass.ps}}} \small} \hfill \end{figure}$

Wie anhand der Abbildungen leicht zu erkennen ist, verschiebt der Tiefpaß die Phase nach hinten, der Hochpaß nach vor während sie der Mittelwertfilter unverändert läßt.

Die Frequenzgänge, also die Verhältnisse zwischen Eingangs- und Ausgangsamplituden einer angelegten Sinusschwingung der Kreisfrequenz $\omega$ , von Tief-, Hoch- und Bandpaß sind in Tabelle 2.5.1 angegeben.

**Abbildung:** **Frequenzgänge**
$\begin{figure}\centerline {\fbox{ $\begin{array}{l @{\hspace{6mm}} l @{\;:\;} l}... ..._0^2-\omega^2)^2+4 \Gamma^2 \omega^2}} \\ [2mm] \end{array}$}}\small\end{figure}$

Für den Fall einer Filterfrequenz von 1000 Hz sind die Frequenzgänge in den Abb. 12 - 14 graphisch dargestellt.

**Abbildung 12:** **Frequenzgang TP**
**Abbildung 13:** **Frequenzgang HP**
$\begin{figure} \hfill \parbox {70mm}{\centerline{\fbox{\epsffile{low1000.ps}}}... ... {70mm}{\centerline{\fbox{\epsffile{high1000.ps}}} \small} \hfill \end{figure}$

**Abbildung 14:** **Frequenzgang BP**
$\begin{figure} \centerline {\fbox{\epsffile{bnd1k200.ps}}} \small\end{figure}$

Lineare Transformationen

Mittels der Optionen -g $\langle$ gain $\rangle$ und -a $\langle$ bias $\rangle$ kann eine einfache lineare Transformation der Form $y=gain \times x+ bias$ durchgeführt werden. Wird die Option -c gewählt, so wird $\langle$ bias $\rangle$ automatisch so gewählt, daß der Durchschnittswert $\bar{a}=0$ . Die Option -y normiert die erzeugte Datei sodaß $\max y = -\min y = 1$ . Werden die Optionen -c und -n gemeinsam verwendet, so wird der Output bei maximaler Aussteuerung zentriert, also $\bar{a} = 0 \wedge ( \max y = 1 \vee \min y = -1)$ .

Die Option -r vertauscht die Reihenfolge der

, spielt also die Datei verkehrt ab. Die Option -i negiert alle Werte (