This section describes Shor's algorithm from a functional point of view which means that it doesn't deal with the implementation for a specific hardware architecture. A detailed implementation for the Cirac-Zoller device can be found in [8]. For a more rigid mathematical description, please refer to [9].
Let ![]() with the greatest common divisor
with the greatest common divisor
![]() be the number to be factorised,
be the number to be factorised, ![]() a
randomly selected number relatively prime to
a
randomly selected number relatively prime to ![]() (i.e.
(i.e.
![]() and
and ![]() the following function with the
period
the following function with the
period ![]() :
:
The function ![]() performs a modular exponentiation,
its period
performs a modular exponentiation,
its period ![]() is the order of
is the order of
![]() .
If
.
If ![]() is even, we can define a
is even, we can define a ![]() , which satisfies
the condition
, which satisfies
the condition
![]() and therefore is the
solution of one of the following systems of equations:
and therefore is the
solution of one of the following systems of equations:
The first two systems have the trivial solutions ![]() and
and ![]() which don't differ from those of the quadratic equation
which don't differ from those of the quadratic equation ![]() in
in ![]() or a Galois field
or a Galois field ![]() (i.e.
(i.e. ![]() with prime
with prime ![]() ).
The last two systems have the non-trivial solutions
).
The last two systems have the non-trivial solutions ![]() ,
, ![]() ,
as postulated by the Chinese remainder theorem stating that
a system of
,
as postulated by the Chinese remainder theorem stating that
a system of ![]() simultaneous congruences (i.e. a system of equations of
the form
simultaneous congruences (i.e. a system of equations of
the form
![]() ) with coprime moduli
) with coprime moduli
![]() (i.e.
(i.e.
![]() for all
for all ![]() )
has a unique solution
)
has a unique solution ![]() with
with
![]() .
.
If ![]() is even and
is even and ![]() with
with ![]() and
and ![]() ,
then
,
then ![]() or
or ![]() must have a common divisor with
must have a common divisor with ![]() because
because
![]() which means that
which means that ![]() with
with
![]() and therefore
and therefore
![]() .
A factor of
.
A factor of ![]() can then be found by using Euclid's algorithm
for determing
can then be found by using Euclid's algorithm
for determing
![]() and
and
![]() which is
defined as
which is
defined as
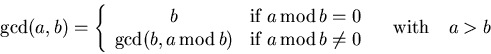
It can be shown that a random ![]() matches the above mentioned
conditions with a probability
matches the above mentioned
conditions with a probability
![]() if
if ![]() is not
of the form
is not
of the form ![]() or
or ![]() .
Since there are efficient classical algorithms to factorise pure
prime powers (and of course to recognise a factor of 2), an
efficient probabilistic algorithm for factorisation can be found
if the period
.
Since there are efficient classical algorithms to factorise pure
prime powers (and of course to recognise a factor of 2), an
efficient probabilistic algorithm for factorisation can be found
if the period ![]() of the modular exponentiation can be determined
in polynomial time.
of the modular exponentiation can be determined
in polynomial time.
Let ![]() be an operator of the form
be an operator of the form
![]() and
and
![]() a function with the
unknown period
a function with the
unknown period ![]() .
.
To determine ![]() , we need two registers, with the sizes of
, we need two registers, with the sizes of
![]() and
and ![]() qubits, which should be reset to
qubits, which should be reset to
![]() .
.
As a first step we produce a homogenous superposition of all
basevectors in the first register by applying an operator ![]() with
with
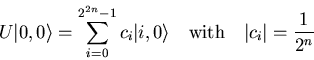
This can e.g. be achieved by transforming each qubit with the
![]() operator (see section 2.1.2).
Another possibility is the discrete fast Fourier
transform (
operator (see section 2.1.2).
Another possibility is the discrete fast Fourier
transform (![]() ) which is defined for
) which is defined for ![]() qubits as
qubits as
Applying ![]() to the resulting state gives
to the resulting state gives
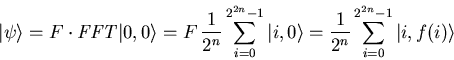
A measurement of the second register with the result ![]() with
with ![]() reduces the state to
reduces the state to
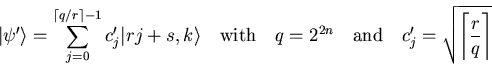
The post-measurement state
![]() of the first register
consists only of basevectors of the form
of the first register
consists only of basevectors of the form
![]() since
since
![]() for all
for all ![]() .
It therefore has a discrete, homogenous spectrum.
.
It therefore has a discrete, homogenous spectrum.
It is not possible to directly extract the period ![]() or a
multiple of it by measurement of the first register because
of the random offset
or a
multiple of it by measurement of the first register because
of the random offset ![]() .
The result of a Fourier transform, however, is invariant
(except for phase factors which don't effect the probability
spectrum) to offsets of a periodic distribution.
.
The result of a Fourier transform, however, is invariant
(except for phase factors which don't effect the probability
spectrum) to offsets of a periodic distribution.
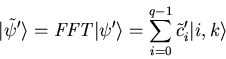
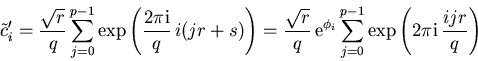
If ![]() is a multiple of
is a multiple of ![]() then
then
![]() if
if ![]() is a
multiple of
is a
multiple of ![]() and
and ![]() otherwise.
But even if
otherwise.
But even if ![]() is not a power of
is not a power of ![]() , the spectrum of
, the spectrum of
![]() shows distinct peaks with a
period of
shows distinct peaks with a
period of ![]() because
because
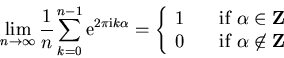
This is also the reason why we use a first register of ![]() qubits when
qubits when ![]() because it guarantees at least
because it guarantees at least ![]() elements in the above sum and thus a peak width of
order
elements in the above sum and thus a peak width of
order ![]() .
.
If we now measure the first register we will get a value ![]() close to
close to ![]() with
with
![]() .
This can be written as
.
This can be written as
![]() .
We can think of this as finding a rational approximation
.
We can think of this as finding a rational approximation
![]() with
with ![]() for the fixed point binary number
for the fixed point binary number
![]() .
An an efficient classical algorithm for solving this problem
using continued fractions is described in [10] and
also implemented in the program shor (see section 4.3).
.
An an efficient classical algorithm for solving this problem
using continued fractions is described in [10] and
also implemented in the program shor (see section 4.3).
Since the form of a rational number is not unique, ![]() and
and
![]() are only determined by
are only determined by
![]() if
if
![]() .
The probability that
.
The probability that ![]() and
and ![]() are coprime is greater
then
are coprime is greater
then ![]() , so only
, so only ![]() tries are necessary for
a constant probability of success as close at 1 as desired.
tries are necessary for
a constant probability of success as close at 1 as desired.