Quantum States and Operators

The Hilbert Space

The state of a quantum computer with $n$ qubits is a point in a $2^n$-dimensional Hilbert space ${\cal H}={\bf C}^{2^n}$. The theoretical storage capacity therefore increases exponentially with the number of qubits.

Any computational step can be described as an operator $O: {\vert\psi \rangle} \to {\vert\phi \rangle}$ over ${\cal H}$ or a subspace of ${\cal H}$ which transforms the input state ${\vert\psi \rangle}$ to the output state ${\vert\phi \rangle}={\vert O\,\psi \rangle}$.

Unitary Operators

As pointed out in (section 1.2.4), quantum computers can only perform reversible operations. Every reversible operation can be described by a unitary operator $U$ which matches the condition $U^{-1}=U^\dagger$. Compositions of unitary operators are also unitary since $(UV)^{-1}= V^\dagger U^\dagger$.

A general unitary transformation in the two dimensional Hilbert space ${\bf C}^2$ can be defined as follows:

$${\it U2}(\theta,\delta,\sigma,\tau)={\left(\begin{array}{c c}... ...\quad{\rm with}\quad \theta, \delta, \sigma, \tau \in {\bf R}$$

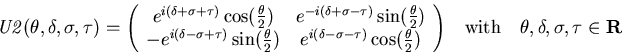
If this operator can be applied to arbitrary 2-dimensional subspaces of ${\cal H}$, than any unitary transformation can be constructed by composition. If only subspaces corresponding to a subset of qubits are allowed, which is the case for many proposed architectures, among them also the linear ion trap ( Cirac-Zoller device), then an additional 4-dimensional 2-qubit operator is needed to obtain a mixing between separate qubits [2].

One possibility for this operator is the 2-qubit XOR which is defined as $mxor: {\vert x,y \rangle} \to {\vert x,x \oplus y \rangle}$ or in matrix notation:

$${\it XOR}={\left(\begin{array}{c c c c}1&0&0&0\\ 0&1&0&0\\ 0&0&0&1\\ 0&0&1&0\end{array}\right)}$$

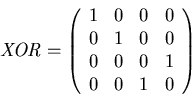
A quantum computer which is capable of performing ${\it U2}$ and ${\it XOR}$ operations can therfore perform any possible operation and is in this sense universal.