Input and Output

Initial State

To set a quantum computer to the desired input state ${\vert\psi \rangle}$, it suffices to provide means to initially ``cool'' all qubits to ${\vert \rangle}$ and then apply a unitary transformation $U$ which matches the condition $U {\vert \rangle} = {\vert\psi \rangle}$. One might think of $U$ as a base transformation which trivially exists for any desired ${\vert\psi \rangle}$.

Measuring States

Measuring $n$ qubits reduces the dimensionality of ${\cal H}$ by a factor of $2^n$. The outcome of the measurement is biased by the probability amplitude for a certain bit configuration.

Consider two quantum registers with $n$ and $m$ qubits in the state

$${\vert\psi \rangle}=\sum_{i=0}^{2^n-1} \sum_{j=0}^{2^m-1} c_{... ...\rangle} \quad{\rm with}\quad \sum_{i,j} c_{i,j}c_{i,j}^* = 1$$

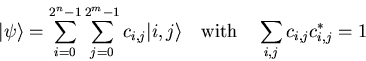
The basevectors ${\vert i,j \rangle}$ are interpreted as a pair of binary numbers with $i<2^n$ and $j<2^m$. The probability $p(I)$ to measure the number $I$ in the first register and the according post measurement state ${\vert\psi_I' \rangle}$ are given by

$$p(I)=\sum_{j=0}^{2^m-1} c_{I,j} c_{I,j}^*, \quad{\rm and}\qua... ...1}{\sqrt{p(I)}} \sum_{j=0}^{2^m-1} c_{I,j} {\vert I,j \rangle}$$

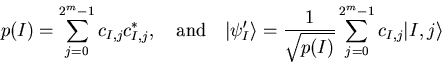
The measurement of qubits is the only non unitary operation, a quantum computer must be able to perform during calculation.