


Next: Bibliography
Up: Shor's Algorithm for Quantum
Previous: The Algorithm
Contents
Subsections
The program shor
The program shor is an implementation of Shor's algorithm
using the library QULIB to simulate an abstract quantum computer.
It is written in C++ under Linux and should run on every computer
with an ANSI C++ compiler.
For an overview of the used functions and a summary of the main
program please refer to appendix B.
shor is started from the command line with
shor <number> [options]
The first parameter is the number to be factorised.
The following options are supported:
- -s seed
- sets the seed value for the pseudo random number
generator needed for the simulation of measurements and
the selection of the base value
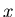 (see section 4.2.1).
(see section 4.2.1).
Any value from 0 to 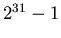 is allowed.
If no seed value is provided, the actual system clock is used.
is allowed.
If no seed value is provided, the actual system clock is used.
- -t maxtries
- sets the maximum numbers of selections (i.e.
measurements without state reduction) from the same
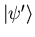 state in case of failure.
state in case of failure.
Of course, this would not be possible on a real quantum
computer, but it can be interpreted as repeating the
computation with the same 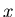 value (see section 4.2.1)
and ``by chance'' measuring the same value in the second
register.
value (see section 4.2.1)
and ``by chance'' measuring the same value in the second
register.
The default value for this option is 3.
If you prefer a more ``realistic'' simulation, set the value to 1
and after every failure the whole simulation is restarted from
scratch.
- -g gates
- sets the maximum number of conditional phase gates
per bit used in the implementation of the fast Fourier transform
(see [8] for details).
A lower number means that the 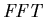 is less accurate but
carried out faster (
is less accurate but
carried out faster (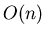 instead of
instead of 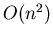 elementary
operators).
There is a tradeoff between faster execution and higher
probability of failure due to less accurate peaks in the
spectrum (see section 4.2.3).
elementary
operators).
There is a tradeoff between faster execution and higher
probability of failure due to less accurate peaks in the
spectrum (see section 4.2.3).
This option is realistic in the sense that it could be
implemented on a real quantum computer.
If no value is given, the 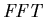 is carried out exactly.
is carried out exactly.
- -q (operate quietly)
- No log output is produced and only the result of the
factorisation is printed.
- -v (operate verbosely)
- Every step of the algorithm commented.
- -l (log spectrums)
- After each operation or measurement the
spectrum of the quantum registers is printed.
- -d (dump states)
- After each operation or measurement the
state of the quantum registers is printed
When called with an illegal syntax, shor produces a USAGE
message.
When a number is cannot be factorised with Shor's algorithm,
the program terminates with an explaining message:
number must be odd !
81 is a prime power of 3 !
59 is a prime number !
15 is the smallest number which can be factorised with Shor's
algorithm.
The command shor 15 -v -t1 -s7 starts the simulation in
verbose mode with a random seed value of 7
and immediate recalculation in case of failure.
The following output is produced:
factoring 15: random seed = 7, tries = 1.
allocating 12 quBits with 256 terms.
RESET: reseting state to |0,0>
FFT: performing 1st Fourier transformation.
EXPN: trying x = 2. |a,0> --> |a,2^a mod 15>
MEASURE: 2nd register: |*,1>
FFT: performing 2nd Fourier transformation.
MEASURE: 1st register: |0,1>
<failed> measured zero in 1st register. trying again ...
RESET: reseting state to |0,0>
FFT: performing 1st Fourier transformation.
EXPN: trying x = 8. |a,0> --> |a,8^a mod 15>
MEASURE: 2nd register: |*,4>
FFT: performing 2nd Fourier transformation.
MEASURE: 1st register: |64,4>
rational approximation for 64/2^8 is 1/4, possible period: 4
8^2 mod 15 = 4. possible common factors of 15 with 5 and 3.
15 = 5 * 3.
program succeeded after 1 s and 2 iterations.
The first try failed because 0 was measured in the first
register of
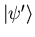 and
and
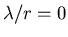 gives no
information about the period
gives no
information about the period 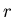 .
.
One might argue that this is not likely to happen, since the
first register has 8 qubits which would suggest a probability
of 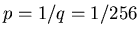 to measure 0.
In fact, if a number
to measure 0.
In fact, if a number 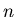 is to be factored, one might expect
a period about
is to be factored, one might expect
a period about 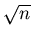 assuming that the prime factors of
assuming that the prime factors of
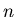 are of the same order of magnitude.
This would lead to a period
are of the same order of magnitude.
This would lead to a period 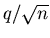 after the
after the  or
or  .
.
In the special case of a start value 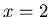 the period of
modular exponentiation is 4 since
the period of
modular exponentiation is 4 since
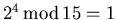 ,
consequently the Fourier spectrum shows 4 peaks at
,
consequently the Fourier spectrum shows 4 peaks at
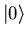 ,
, 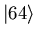 ,
,
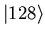 and
and
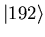 and
and
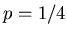 as expected.
This can be verified by running shor with the option
-l.
as expected.
This can be verified by running shor with the option
-l.
The second try also had the same probability of failure since
8 is the multiplicative inverse to 2 in 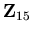 , but
this time, the measurement picked the second peak in the
spectrum at
, but
this time, the measurement picked the second peak in the
spectrum at 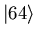 .
With
.
With
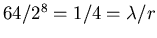 , the period
, the period 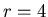 was correctly
identified and the possible common factors
was correctly
identified and the possible common factors
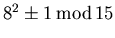 with 15 have been found.
with 15 have been found.



Next: Bibliography
Up: Shor's Algorithm for Quantum
Previous: The Algorithm
Contents
(c) Bernhard Ömer - oemer@tph.tuwien.ac.at - http://tph.tuwien.ac.at/~oemer/
![]() is allowed.
If no seed value is provided, the actual system clock is used.
is allowed.
If no seed value is provided, the actual system clock is used.![]() value (see section 4.2.1)
and ``by chance'' measuring the same value in the second
register.
value (see section 4.2.1)
and ``by chance'' measuring the same value in the second
register.
![]() is less accurate but
carried out faster (
is less accurate but
carried out faster (![]() instead of
instead of ![]() elementary
operators).
There is a tradeoff between faster execution and higher
probability of failure due to less accurate peaks in the
spectrum (see section 4.2.3).
elementary
operators).
There is a tradeoff between faster execution and higher
probability of failure due to less accurate peaks in the
spectrum (see section 4.2.3).
![]() is carried out exactly.
is carried out exactly.