In contrast to finding and multiplying of large prime numbers,
no efficient classical algorithm for the factorization of large
number is known.
An algorithm is called efficient if its execution time i.e. the number
of elementary operations is assymtotically polynomial in the length
of its input measured in bits.
The best known (or at least published) classical algorithm (the
quadratic sieve) needs
![]() operations for factoring a
binary number of
operations for factoring a
binary number of ![]() bits [12] i.e. scales exponentially
with the input size.
bits [12] i.e. scales exponentially
with the input size.
The multiplication of large prime numbers is therefore a one-way function i.e. a function which can easily be evaluated in one direction, while its inversion is practically impossible. One-way functions play a major roll in cryptography and are essential to public key crypto-systems where the key for encoding is public and only the key for decoding remains secret.
In 1978, Rivest, Shamir and Adleman developed a cryptographic algorithm based on the one-way character of multiplying two large (typically above 100 decimal digits) prime numbers. The RSA method (named after the initials of their inventors) became the most popular public key system and is implemented in many communication programs.
While it is generally believed (although not formally proved) that efficient prime factorization on a classical computer is impossible, an efficient algorithm for quantum computers has been proposed in 1994 by P.W. Shor [11].
This section describes Shor's algorithm from a functional point of view which means that it doesn't deal with the implementation for a specific hardware architecture. A detailed implementation for the Cirac-Zoller gate can be found in [13], for a more rigid mathematical description, please refer to [15] and for a more detailed dicussion of the QCL implementation, look at [25].
Let ![]() with the greatest common divisor
with the greatest common divisor
![]() be the number to be factorized,
be the number to be factorized, ![]() a
randomly selected number relatively prime to
a
randomly selected number relatively prime to ![]() (i.e.
(i.e.
![]() and
and ![]() the
modular exponentiation function with the
period
the
modular exponentiation function with the
period ![]() :
:
| (4.19) |
| (4.20) | |||
If ![]() is even and
is even and ![]() with
with ![]() and
and ![]() ,
then
,
then ![]() or
or ![]() must have a common divisor with
must have a common divisor with ![]() because
because
![]() which means that
which means that ![]() with
with
![]() and therefore
and therefore
![]() .
A factor of
.
A factor of ![]() can then be found by using Euclid's algorithm
to determine
can then be found by using Euclid's algorithm
to determine ![]() and
and ![]() which is
defined as
which is
defined as
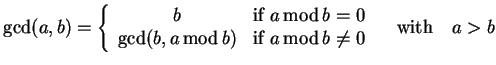 |
(4.21) |
Let ![]() be quantum function
be quantum function
![]() of the integer function
of the integer function
![]() with the
unknown period
with the
unknown period ![]() .
.
To determine ![]() , we need two registers, with the sizes of
, we need two registers, with the sizes of
![]() and
and ![]() qubits, which should be reset to
qubits, which should be reset to
![]() .
.
As a first step we produce a homogenous superposition of all
base-vectors in the first register by applying an operator ![]() with
with
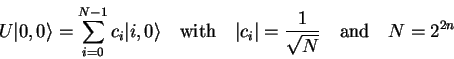 |
(4.22) |
This can e.g. be achieved by the Hadamard transform ![]() .
Applying
.
Applying ![]() to the resulting state gives
to the resulting state gives
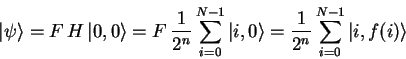 |
(4.23) |
A measurement of the second register with the result ![]() with
with ![]() reduces the state to
reduces the state to
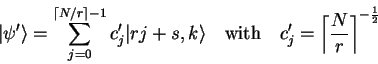 |
(4.24) |
The post-measurement state
![]() of the first register
consists only of base-vectors of the form
of the first register
consists only of base-vectors of the form
![]() since
since
![]() for all
for all ![]() .
It therefore has a discrete, homogenous spectrum.
.
It therefore has a discrete, homogenous spectrum.
It is not possible to directly extract the period ![]() or a
multiple of it by measurement of the first register because
of the random offset
or a
multiple of it by measurement of the first register because
of the random offset ![]() .
This problem can be solved by performing a discrete Fourier
transform (see 4.2.3)
.
This problem can be solved by performing a discrete Fourier
transform (see 4.2.3)
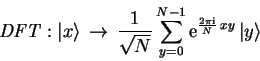 |
(4.25) |
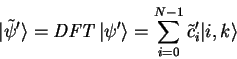 |
(4.26) |
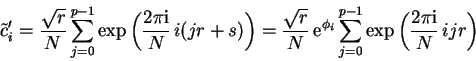 |
(4.27) |
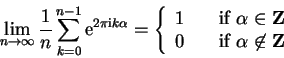 |
(4.28) |
If we now measure the first register, we will get a value ![]() close to
close to ![]() with
with
![]() .
This can be written as
.
This can be written as
![]() .
We can think of this as finding a rational approximation
.
We can think of this as finding a rational approximation
![]() with
with ![]() for the fixed point binary number
for the fixed point binary number
![]() .
An efficient classical algorithm for solving this problem
using continued fractions is described in [16]
and is implemented in the denominator function
(appendix B.2).
.
An efficient classical algorithm for solving this problem
using continued fractions is described in [16]
and is implemented in the denominator function
(appendix B.2).
Since the form of a rational number is not unique, ![]() and
and
![]() are only determined by
are only determined by
![]() if
if
![]() .
The probability that
.
The probability that ![]() and
and ![]() are coprime is greater
then
are coprime is greater
then
![]() , so only
, so only ![]() tries are necessary for
a constant probability of success as close at 1 as
desired.4.1
tries are necessary for
a constant probability of success as close at 1 as
desired.4.1
For a ![]() dimensional vector
dimensional vector
![]() , the discrete
Fourier transform is defined as
, the discrete
Fourier transform is defined as
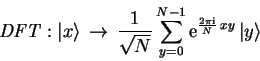 |
(4.29) |
As suggested by Coppersmith [7],
the same principle could adapted be to quantum computers
by using a combination of Hadamard transformations ![]() (see 3.4.4.3) and conditional phase gates
(see 3.4.4.3) and conditional phase gates ![]() (see 3.4.4.4).
The indices below indicate the qubits operated on:
(see 3.4.4.4).
The indices below indicate the qubits operated on:
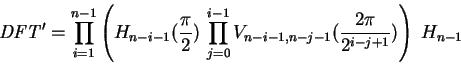 |
(4.30) |
The base-vectors of the transformed state
![]() are given in reverse
bit order, so to get the actual
are given in reverse
bit order, so to get the actual ![]() , the bits
have to be flipped.
, the bits
have to be flipped.
operator dft(qureg q) { // main operator
const n=#q; // set n to length of input
int i; int j; // declare loop counters
for i=0 to n-1 {
for j=0 to i-1 { // apply conditional phase gates
CPhase(2*pi/2^(i-j+1),q[n-i-1] & q[n-j-1]);
}
Mix(q[n-i-1]); // qubit rotation
}
flip(q); // swap bit order of the output
}
|
The most difficult part in implementing Shor's algorithm is
the construction of an efficient quantum function for
modular exponentiation.
| (4.31) |
Assuming we already have an implementation for modular
addition, we could use it to construct modular
multiplication and finally exponentiation since
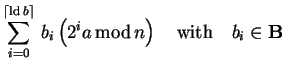 |
(4.32) | ||
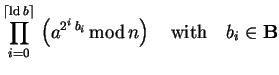 |
(4.33) |
The addition modulo ![]() of a classic integer
of a classic integer ![]() and
a quantum register
and
a quantum register ![]() can result in either
can result in either
![]() or
or ![]() , depending on the particular
base-vector
, depending on the particular
base-vector ![]() .
.
While for ![]() the operation is revertible, this is not
the case for
the operation is revertible, this is not
the case for ![]() , so, if
, so, if ![]() doesn't happen
to be a power of
doesn't happen
to be a power of ![]() , besides the target resister
, besides the target resister
![]() for the sum, we need an additional flag-qubit
for the sum, we need an additional flag-qubit
![]() to allow for a quantum function addn
which is both, unitary and invariant to
to allow for a quantum function addn
which is both, unitary and invariant to ![]() :
:
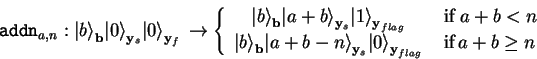 |
(4.34) |
Since
![]() is a quantum function for
modular subtraction and thus implements the inverse function
is a quantum function for
modular subtraction and thus implements the inverse function
![]() to
to
![]() ,
we can construct an overwriting version oaddn
of modular addition, by using the method introduced
in 3.5.2.3:
,
we can construct an overwriting version oaddn
of modular addition, by using the method introduced
in 3.5.2.3:
| (4.35) |
| (4.36) |
qufunct oaddn(int a,int n,qureg sum,quconst e) {
qureg j[#sum];
qureg f[1];
addn(a,n,sum,f,j,e); // junk -> a+b mod n
Swap(sum,j); // swap junk and sum
CNot(f,e); // toggle flag
!addn(n-a,n,sum,f,j,e); // uncompute b to zero
}
|
Modular multiplication is merely a composition of conditional
additions for each qubit of ![]() .
The first summand can be slightly optimized, since the
accumulator (prod) is still empty.
.
The first summand can be slightly optimized, since the
accumulator (prod) is still empty.
qufunct muln(int a,int n,quconst b,qureg prod,quconst e) {
int i;
for i=0 to #prod-1 {
if bit(a,i) { CNot(prod[i],b[0] & e); }
}
for i=1 to #b-1 {
oaddn(2^i*a mod n,n,prod,b[i] & e);
}
}
|
By using two conditional XOR gates defined as
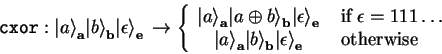 |
(4.37) |
| (4.38) |
qufunct omuln(int a,int n,qureg b,quconst e) {
qureg j[#b];
muln(a,n,b,j,e);
!muln(invmod(a,n),n,j,b,e);
cxor(j,b,e);
cxor(b,j,e);
}
|
As with muln, we can construct modular exponentiation by conditionally applying omuln with the qubits of the exponents as enable string. Before we can start the iteration, the accumulator (ex) has to be initialized by 1.
qufunct expn(int a,int n,quconst b,quvoid ex) {
int i;
Not(ex[0]); // start with 1
for i=0 to #b-1 {
omuln(powmod(a,2^i,n),n,ex,b[i]); // ex -> ex*a^2^i mod n
}
}
|
The implementation of the Shor algorithm uses the following functions:
The procedure shor checks whether the integer number is suitable for quantum factorization, and then repeats Shor's algorithm until a factor has been found.
procedure shor(int number) {
int width=ceil(log(number,2)); // size of number in bits
qureg reg1[2*width]; // first register
qureg reg2[width]; // second register
int qmax=2^width;
int factor; // found factor
int m; real c; // measured value
int x; // base of exponentiation
int p; int q; // rational approximation p/q
int a; int b; // possible factors of number
int e; // e=x^(q/2) mod number
|
if number mod 2 == 0 { exit "number must be odd"; }
if testprime(number) { exit "prime number"; }
if testprimepower(number) { exit "prime power"; };
|
{
{ // generate random base
x=floor(random()*(number-3))+2;
} until gcd(x,number)==1;
print "chosen random x =",x;
Mix(reg1); // Hadamard transform
expn(x,number,reg1,reg2); // modular exponentiation
measure reg2; // measure 2nd register
dft(reg1); // Fourier transform
measure reg1,m; // measure 1st register
reset; // clear local registers
|
if m==0 { // failed if measured 0
print "measured zero in 1st register. trying again ...";
} else {
c=m*0.5^(2*width); // fixed point form of m
q=denominator(c,qmax); // find rational approximation
p=floor(q*m*c+0.5);
print "measured",m,", approximation for",c,"is",p,"/",q;
if q mod 2==1 and 2*q<qmax { // odd q ? try expanding p/q
print "odd denominator, expanding by 2";
p=2*p; q=2*q;
}
if q mod 2==1 { // failed if odd q
print "odd period. trying again ...";
} else {
print "possible period is",q;
e=powmod(x,q/2,number); // calculate candidates for
a=(e+1) mod number; // possible common factors
b=(e+number-1) mod number; // with number
print x,"^",q/2,"+ 1 mod",number,"=",a,",",
x,"^",q/2,"- 1 mod",number,"=",b;
factor=max(gcd(number,a),gcd(number,b));
}
}
} until factor>1 and factor<number;
print number,"=",factor,"*",number/factor;
}
|
15 is the smallest number that can be factorized with Shor's
algorithm, as it's the product of the smallest odd prime
numbers ![]() and
and ![]() .
Our implementation of the modular exponentiation needs
.
Our implementation of the modular exponentiation needs
![]() qubits scratch space with
qubits scratch space with
![]() .
The algorithm itself needs
.
The algorithm itself needs ![]() qubits, so a total of 21
qubits must be provided.
qubits, so a total of 21
qubits must be provided.
$ qcl -b21 -i shor.qcl qcl> shor(15) : chosen random x = 4 : measured zero in 1st register. trying again ... : chosen random x = 11 : measured 128 , approximation for 0.500000 is 1 / 2 : possible period is 2 : 11 ^ 1 + 1 mod 15 = 12 , 11 ^ 1 - 1 mod 15 = 10 : 15 = 5 * 3 |
One might argue that this is not likely to happen, since the
first register has 8 qubits and ![]() possible base-vectors,
however, if a number
possible base-vectors,
however, if a number ![]() is to be factored, one might expect
a period about
is to be factored, one might expect
a period about ![]() assuming that the prime factors of
assuming that the prime factors of
![]() are of the same order of magnitude.
This would lead to a period
are of the same order of magnitude.
This would lead to a period
![]() after the
after the ![]() and the probability
and the probability
![]() to accidentally
pick the basevector
to accidentally
pick the basevector ![]() , would be
, would be ![]() .
.
In the special case of a start value ![]() the period of the
modular exponentiation is 2 since
the period of the
modular exponentiation is 2 since
![]() ,
consequently the Fourier spectrum shows 2 peaks at
,
consequently the Fourier spectrum shows 2 peaks at
![]() and
and
![]() and
and ![]() .
.
The second try also had the same probability of failure since
![]() , but this time, the measurement picked the
second peak in the spectrum at
, but this time, the measurement picked the
second peak in the spectrum at
![]() .
With
.
With
![]() , the period
, the period ![]() was correctly
identified and the factors
was correctly
identified and the factors
![]() to 15 have been found.
to 15 have been found.