As has been shown in 3.1.2, quantum computers and probabilistic classical computers are computationally equivalent, but for certain tasks, quantum algorithms can provide a more efficient solution than classical implementations.
In order to achieve any speedup over classical algorithms, it is necessary to take advantage of the unique features of quantum computing namely
A key element in any universal programming language is
conditional branching.
Any classical program can be modeled as a decision tree
where each node corresponds to a binary state ![]() and leads
to one or more successor states
and leads
to one or more successor states ![]() .
On a deterministic Turing machine (TM), only one of those
transitions
.
On a deterministic Turing machine (TM), only one of those
transitions
![]() is possible, so the computational
path
is possible, so the computational
path
![]() is predetermined.
is predetermined.
On a probabilistic TM, the transitions are characterized by
probabilities ![]() with
with ![]() and one of the possible
successor states
and one of the possible
successor states ![]() is chosen accordingly at random.
is chosen accordingly at random.
Since the eigenvectors ![]() directly correspond to classical
binary states, we might interpret a unitary transformation
directly correspond to classical
binary states, we might interpret a unitary transformation
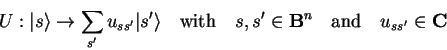 |
(3.37) |
| (3.38) |
Most non-classical algorithms take advantage of this feature by bringing a register into a even superposition of eigenstates to serve as search space. This can be achieved by applying the Hadamard transformation (see 3.4.4.3) to each qubit
[0/4] 1 |0000> qcl> qureg q[2]; // allocate 2-qubit register qcl> Mix(q[0]); // rotate first qubit [2/4] 0.707107 |0000> + 0.707107 |0001> qcl> Mix(q[1]); // rotate second qubit [2/4] 0.5 |0000> + 0.5 |0010> + 0.5 |0001> + 0.5 |0011> |
Since the Hadamard transforms for each single qubit commute, we can a-posteriori emulate classic probabilistic behavior by performing a measurement on the single qubits; thereby, the temporal order of the measurements is unimportant so we can force a decision on the second qubit before we decide on the the first and reconstruct the classical computational path in reverse
qcl> measure q[1]; // second qubits gives 0 [2/4] 0.707107 |0000> + 0.707107 |0001> qcl> measure q[0]; // first qubit gives 1 [2/4] 1 |0001> |
If we restrict unitary transformations to pseudo-classic
operators (see 2.2.2.4) then the classical
decision tree degenerates into a list and we end up with
the functionality of a classical reversible computer i.e.
for any bijective binary function ![]() there is a corresponding
pseudo-classic operator
there is a corresponding
pseudo-classic operator
| (3.39) |
| (3.40) |
However, if we use a quantum function on an superposition
of eigenstates, the same classical computation is performed
on all bit-strings simultaneously.
| (3.41) |
As an example, lets consider a full binary adder
| (3.42) |
| (3.43) |
qcl> qureg a[1]; // argument a qcl> qureg b[1]; // argument b qcl> qureg s[2]; // target register s=a+b qcl> Mix(a & b); // bring arguments into superposition [4/4] 0.5 |0000> + 0.5 |0010> + 0.5 |0001> + 0.5 |0011> qcl> CNot(s[0],a); // calculate low bit of sum [4/4] 0.5 |0000> + 0.5 |0010> + 0.5 |0101> + 0.5 |0111> qcl> CNot(s[0],b); [4/4] 0.5 |0000> + 0.5 |0110> + 0.5 |0101> + 0.5 |0011> qcl> CNot(s[1],a & b); // calculate high bit of sum [4/4] 0.5 |0000> + 0.5 |0110> + 0.5 |0101> + 0.5 |1011> |
While superpositioning and quantum parallelism allow us to perform an exponentially large number of classical computations in parallel, the only way to read out any results is by performing a measurement whereby all but one of the superpositioned eigenstates get discarded. Since it doesn't make any difference if the computational path is determined during the calculation (as with the probabilistic TM) or a-posteriori (by quantum measurement), the use of quantum computers wouldn't provide any advantage over probabilistic classical computers.
Quantum states, however, are not merely a probability
distribution of binary values but are vectors i.e.
each eigenstate in a superposition isn't characterized
by a real probability, but a complex amplitude, so
| (3.44) |
So, while on a probabilistic TM, the probabilities of
two different computational paths leading to the same
final state ![]() simply add up, this is not necessarily
the case on a quantum computer since generally
simply add up, this is not necessarily
the case on a quantum computer since generally
| (3.45) |
To illustrate this concept, consider the three states
| (3.46) |
| (3.47) |
| (3.48) |
So while the computational paths on a probabilistic TM are independent, interference allows computations on superpositioned states to interact and it is this interaction which allows a quantum computer to solve certain problems more efficiently than classical computers. The foremost design principle for any quantum algorithm therefor is to use interference to increase the probability of ``interesting'' eigenstates while trying to reduce the probability of ``dull'' states, in order to raise the chance that a measurement will pick one of the former.
Since any unitary operator ![]() can also be regarded as a
base-transformation (see 1.3.2.6), the above
problem can also be reformulated as finding an appropriate
observable for the measurement, thereby effectively replacing
the register observable
can also be regarded as a
base-transformation (see 1.3.2.6), the above
problem can also be reformulated as finding an appropriate
observable for the measurement, thereby effectively replacing
the register observable ![]() (see 2.2.1.5) by an
observable
(see 2.2.1.5) by an
observable
![]() with the Hermitian operator
with the Hermitian operator
| (3.49) |
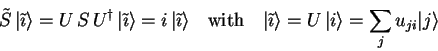 |
(3.50) |
Fourier transformations are esp. useful, if global properties of classic functions such as periodicy are of interest for the problem.
In 2.2.2.5 we have shown that for any non-reversible
boolean function
![]() there exists a set of
unitary quantum functions
there exists a set of
unitary quantum functions
| (3.51) |
While keeping a copy of the argument will allow us to compute non
reversible functions, this also forces us to provide extra storage
for intermediate results.
Since longer calculations usually involve the composition of many
quantum functions this would leave us with a steadily increasing
amount of ``junk'' bits which are of no concern for the final result.
A straightforward implementation of
![]() already uses
3 additional registers (function values are in prefix notation,
already uses
3 additional registers (function values are in prefix notation, ![]() stands for a quantum function
stands for a quantum function
![]() ,
indices indicate the registers operated on):
,
indices indicate the registers operated on):
| (3.52) |
A simple and elegant solution of this problem was proposed by Bennet
[8,9]:
If a composition of two non-reversible functions ![]() is
to be computed, the scratch space for the intermediate result
can be ``recycled'' using the following procedure:
is
to be computed, the scratch space for the intermediate result
can be ``recycled'' using the following procedure:
| (3.53) |
Without scratch-management, the evaluation of a composition of depth
![]() needs
needs ![]() operations and consumes
operations and consumes ![]() junk registers.
Bennet's method of uncomputing can then be used to trade space
against time: Totally uncomputing of all intermediate results
needs
junk registers.
Bennet's method of uncomputing can then be used to trade space
against time: Totally uncomputing of all intermediate results
needs ![]() operations and
operations and ![]() scratch registers, which is useful,
if the scratch can be reused in the further computation.
scratch registers, which is useful,
if the scratch can be reused in the further computation.
By a combined use of ![]() registers as scratch and junk space,
a composition of depth
registers as scratch and junk space,
a composition of depth
![]() can be evaluated with
can be evaluated with
![]() operations.
An calculation of
operations.
An calculation of
![]() on a 4-register machine
(1 input, 1 output and 2 scratch/junk registers) would run as
follows (function values are in prefix notation):
on a 4-register machine
(1 input, 1 output and 2 scratch/junk registers) would run as
follows (function values are in prefix notation):
| (3.54) |
If the computation of a function ![]() fills a scratch register with the
junk bits
fills a scratch register with the
junk bits ![]() (i.e.
(i.e.
![]() ), a
similar procedure can free the register again:
), a
similar procedure can free the register again:
| (3.55) |
| (3.56) |
As pointed out in 2.2.2.4, every invertible function
![]() has a corresponding
pseudo classic operator
has a corresponding
pseudo classic operator
![]() .
While a direct implementation of
.
While a direct implementation of ![]() is possible with any
complete set of pseudo-classic operators3.6,
the implementation as a quantum function can be substantially
more efficient.
is possible with any
complete set of pseudo-classic operators3.6,
the implementation as a quantum function can be substantially
more efficient.
If we have efficient implementations of the quantum functions
![]() and
and
![]() , then an
overwriting operator
, then an
overwriting operator ![]() can be constructed by using an
can be constructed by using an
![]() qubit scratch register.
qubit scratch register.
| (3.57) |