As has been illustrated in 2.1.2, a computer is basically a device which
The way ![]() is actually specified, depends on the computational
model; possibilities vary from explicit enumeration, over
feed forward networks (as in logical circuits) and decision trees
up to finite automatons (as in the Turing machine).
is actually specified, depends on the computational
model; possibilities vary from explicit enumeration, over
feed forward networks (as in logical circuits) and decision trees
up to finite automatons (as in the Turing machine).
A general requirement of any specification method is, that
the mechanism used to produce ![]() must not be more powerful or
complex than the machine it is executed on, which would defy
the purpose of using a computer in the first place.
must not be more powerful or
complex than the machine it is executed on, which would defy
the purpose of using a computer in the first place.
As has been pointed out in 2.3.4, QPLs use a classical
universal programming language to define the actual sequence
![]() of instructions for a quantum computer.
According to the above criterion, this approach is useful, only if
quantum computers are at least as powerful as universal
classical computers.
of instructions for a quantum computer.
According to the above criterion, this approach is useful, only if
quantum computers are at least as powerful as universal
classical computers.
If we consider a quantum computer with the Toffoli gate
(see 2.2.2.4) as the only available instruction,
then any transformation of the machine state has to be of the
form
| (3.1) |
A general boolean function ![]() over
over ![]() , can be
implemented by using a pseudo-classical operator
, can be
implemented by using a pseudo-classical operator ![]()
| (3.2) |
So any classically computable function ![]() can also be implemented
on a quantum computer.
Moreover, C. H. Bennet has shown that a reversible implementation
of
can also be implemented
on a quantum computer.
Moreover, C. H. Bennet has shown that a reversible implementation
of ![]() can be done with a maximal overhead of
can be done with a maximal overhead of ![]() in time and
in time and
![]() in space complexity (see 3.5.2). [8]
in space complexity (see 3.5.2). [8]
On the other hand, as a general ![]() -qubit quantum state consists
of maximally
-qubit quantum state consists
of maximally ![]() eigenstates with a non-zero amplitude and
unitary transformations take the form of linear operators and
consequently can be described as
eigenstates with a non-zero amplitude and
unitary transformations take the form of linear operators and
consequently can be described as
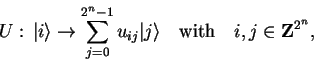 |
(3.3) |
Due to the stochastic nature of quantum measurements, the emulating computer will also need a source of true randomness (like e.g. the probabilistic Turing machine).
So QPLs can be regarded as a meta-programming languages, as a program isn't intended to run on a quantum computer itself, but on a (probabilistic) classical computer which in turn controls a quantum computer. In the terms of classical computer science, you can describe this setting as a universal computer with a quantum oracle. Figure 3.1 illustrates this hybrid architecture.
From the perspective of the user, quantum programs behave exactly like any other classical program, in the sense that it takes classical input such as startup parameters or interactive data, and produces classical output. The state of the controlling computer (i.e. program counter, variable values, but also the mapping of quantum registers) is also strictly classical and referred to as program state.
The actual program ![]() , i.e. the sequence of quantum instructions
consisting of elementary gates, measurement- and
initialization-instructions is passed over a well defined interface
to the quantum computer, while
the returned output of is restricted to binary measurements values.
The quantum computer doesn't require any control logic, it's
computational state can therefor be fully described by the common
quantum state
, i.e. the sequence of quantum instructions
consisting of elementary gates, measurement- and
initialization-instructions is passed over a well defined interface
to the quantum computer, while
the returned output of is restricted to binary measurements values.
The quantum computer doesn't require any control logic, it's
computational state can therefor be fully described by the common
quantum state ![]() of its qubits, also referred to as machine
state.
of its qubits, also referred to as machine
state.