The Hilbert space ![]() of a quantum computer with
of a quantum computer with ![]() qubits has
qubits has
![]() dimensions.
The basevectors of
dimensions.
The basevectors of ![]() are bitstrings of the length
are bitstrings of the length ![]() , which
are represented by the class bitvec.
, which
are represented by the class bitvec.
If the wordlength ![]() of the computer is smaller than
of the computer is smaller than ![]() , then
an array is dynamically allocated; if it
, then
an array is dynamically allocated; if it ![]() , the vector is
stored as an unsigned int, which is considerably faster and
should suffice for most applications.
, the vector is
stored as an unsigned int, which is considerably faster and
should suffice for most applications.
A quantum state
![]() of
of ![]() qubits can be described
by
qubits can be described
by ![]() complex numbers.
complex numbers.
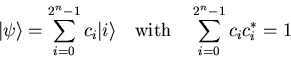
Only terms with ![]() must be stored, which can considerably
reduce the required amount of memory since registers which are
entangled by an arithmetic function (which is normally the case with
all scratch registers) don't require additional entries.
must be stored, which can considerably
reduce the required amount of memory since registers which are
entangled by an arithmetic function (which is normally the case with
all scratch registers) don't require additional entries.
The best datastructure for storing those terms is determined by the
most common forms of access, which, in our case, are sequential read
out and adding of terms, where it is crucial that the time to determine
whether a basevector is already in the list (and the amplitudes
have to be added) and the time fore adding a new entry (if the
basevector in not in the list) are of the order ![]() i.e.
don't increase with the size of the list.
Removing of single elements is normally not needed an may take longer.
i.e.
don't increase with the size of the list.
Removing of single elements is normally not needed an may take longer.
A linear array in combination with a hashtable as index can meet all
these requirements.
A basevector is thereby mapped onto the hashtable by a hashfunction
which provides a pseudo-random distribution.
The entry of the hashtable contains a pointer to the corresponding
entry in the array or indicates that such an entry doesn't exist.
The overhead for the detection and handling of collisions is of order
![]() if the hashtable is considerably longer than the list itself.
if the hashtable is considerably longer than the list itself.
The internal class termlist provides this datastructure with all necessary access function and the ability to dynamically adapt the size of arrays and hashtables by powers of 2. The class quBaseState is the user class representing the common state of all qubits and contains two termlist objects which alternately serve as argument or result of operations.
Since all qubits are entangled, substates can't be represented as an
isolated datastructure, but are merely references to certain
qubits of an associated basestate.
A reference to ![]() qubits of an
qubits of an ![]() qubit basestate represents a subspace
qubit basestate represents a subspace
![]() of
of ![]() .
.
The class quSubState and all its derived classes make this reference transparent to the user i.e. all manipulations on the substate are correctly mapped onto its basestate:
Let
![]() be the
be the ![]() qubit basestate of the
substate
qubit basestate of the
substate
![]() referring to the first
referring to the first ![]() qubits of
qubits of
![]() and
and
![]() a unitary operator
a unitary operator
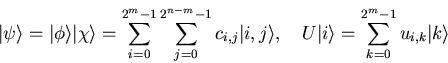
Applying ![]() to
to
![]() would be equivalent to applying
would be equivalent to applying
![]() to
to
![]() where
where ![]() is the identity
operator over
is the identity
operator over ![]() .
.
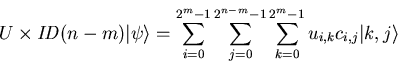
In principle, any unitary operator on ![]() qubits can be represented by a
complex
qubits can be represented by a
complex
![]() matrix.
Applying this operator to a state with
matrix.
Applying this operator to a state with ![]() nonzero terms would
require
nonzero terms would
require ![]() multiplications.
Operators of this kind are represented by the class opMatrix,
which stores the nonzero elements of each row in an array of linear lists.
multiplications.
Operators of this kind are represented by the class opMatrix,
which stores the nonzero elements of each row in an array of linear lists.
Most operators, however, work on limited subspaces of only a few qubits or (as e.g. all arithmetic operators) merely substitute basevectors with or without an additional phase factor. QULIB provides classes for all these special cases:
The class opEmbedded represents operators of the kind
![]() , opPermutation are
operators of the form
, opPermutation are
operators of the form
![]() and are
stored as a one dimensional array of terms.
and are
stored as a one dimensional array of terms.
The class opFunction represents arithmetic functions
of the form
![]() , where
, where
![]() is defined as a virtual member function.
The result of
is defined as a virtual member function.
The result of
![]() is undefined and would lead to an
error.
is undefined and would lead to an
error.
A more general interface for user defined function is the class
opGate for operators of the form
![]() .
The functions
.
The functions ![]() and
and ![]() are provided by the user, who is
responsible that the transformation is unitary.
are provided by the user, who is
responsible that the transformation is unitary.