The Comparator Problem

The comparator problem with the operator $\leq$ is, in comparison with the n-parity problem, very linear in the sense that its error function has no significant local minima. This property makes it a perfect choice for all gradient descend methods like backpropagation and will illustrate the performance gains that can be optained by adding backpropagation features to the standard genetic algorithm.

Backpropagation

To get some reference values for comparisons, two series of 10 sequential backpropagation programs (online learning with $\gamma = 1$), one of which used learning with impulse ($\alpha=0.9$), were started on single transputers. The test problem was a $2\times4$-comparator with the operator $\leq$, the maximal error was 0.001. All programs succeeded and produced the following results ($\overline{x}$ refers to the arithmetic men, $\overline{\Delta x}$ to average deviation from $\overline{x}$ and $\widehat{x}$ to the geometric mean of the samples $x_i$):

impulse	iterations			time
$\alpha$	$\overline{N}$	$\overline{\Delta N}$	$\widehat{N}$	$\overline{T}$	$\overline{\Delta T}$	$\widehat{T}$
0	55.9	9.0	55.3	10.2 s	1.8 s	10.1 s
0.9	235.4	318.0	138.1	53.9 s	72.6 s	31.6 s

Genetic Backpropagation

Six series of 10 programs have been started, the first using the standard genetic algorithm with a population size $p$ of 256, the other five using $b=$ 1, 2, 4, 8 and 16 backpropagation steps per generation with proportional reduced population sizes of 256, 128, 64, 32 and 16. All simulations were run in their parallel versions on a 16 transputer ternary tree using the following configuration file:

par
processor 0 for 16 cmppar -N4 -B12 -e0.001 -g100 -p$p$ -b$b$
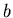
networkis ternarytree
endpar

While all 10 programs with the standard genetic algorithm ($b=0$) failed to train the network to the goal of $E\leq 0.001$ within 100 generations, all programs using the combined algorithm succeeded.

backprop. steps	pop. size	generations			time
$b$	$p$	$\overline{N}$	$\overline{\Delta N}$	$\widehat{N}$	$\overline{T}$	$\overline{\Delta T}$	$\widehat{T}$
1	256	19.9	5.4	19.3	143.3 s	38.9 s	138.9 s
2	128	11.5	3.5	11.1	63.0 s	19.6 s	60.7 s
4	64	4.9	1.0	4.8	22.6 s	4.3 s	22.2 s
8	32	2.9	0.6	2.8	12.3 s	2.6 s	12.0 s
16	16	2.0	0.0	2.0	8.1 s	0.3 s	8.1 s

Fig. 4 shows the average computation time $\overline{T}$ in relation to the number of backpropagation steps in the combined algorithm. The two horizontal lines indicate the average times of the serial backpropagation programs.

Figure 4: Execution Time for 2$\times$4 CMP

While for sequential implementations, the standard backpropagation algorithm would certainly be the better choice for this very problem, the example shows that a parallel implementation of the combined algorithm with a sufficiently high number of backpropagation steps can nevertheless lead to faster execution times even if, as in this case, due to the high linearity of its error function, the problem is perfectly suited for a simple gradient descend method.